このページでは巡回セールスマン問題と呼ばれるNP困難な問題をイジングモデルで表現する方法について述べます。
問題の定式化 #
(まずはハミルトンサイクル問題のページを読んでから、このページを呼んでください。) 無向でも有向でも構わないグラフ \(G = (V, E)\) が与えられます。 また、このグラフの各辺には重み \(W_{uv}\) が定まっているとします。 今、このグラフのハミルトンサイクルであって、サイクル中の辺の重みの総和を最小にするようなハミルトンサイクルを求めたいとしましょう。
この問題はNP困難な問題として知られています。 なお、この問題の判定問題バージョン(サイクルの重みの総和が定数 \(W\) 以下になるようなサイクルは存在するか?)は、NP完全な問題です。
問題の具体例 #
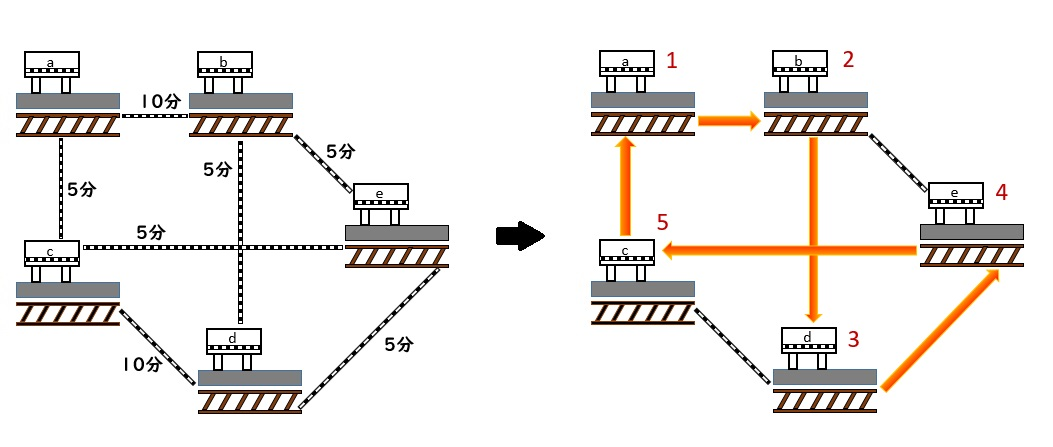
以下の図のような5つの駅と路線があります。各路線を使用した場合の所要時間は以下の通りです。乗り換えにかかる時間は無視できることにします。駅
\(a\)
から出発して、駅
\(b,c,d,e\)
を一度ずつ通って駅
\(a\)
に戻ってくる経路のうち所要時間が最短のものは何でしょうか。答えは図の右側のような
\(a→b→d→e→c→a\)
という経路で、このときの所要時間は30分です。
イジングモデルへの変形 #
この問題を解くためのエネルギー関数は以下のように構築されます。
導入するバイナリ変数はハミルトンサイクル問題の時と同じです。 すなわち、各頂点 \(v\) と、サイクル中の順番 \(i\) に対して、 \(v\) がサイクル中で \(i\) 番目のときに1、そうでないときに0を取るバイナリ変数 \(x_{v,i}\) を設定しておきます。 また、 \(A, B\) を正の定数とします。 ここで、 \(H_A\) はハミルトンサイクル問題のエネルギー関数としましょう。 このとき、巡回セールスマン問題を解くためのエネルギー関数は
\[ H = H_A + H_B \] \[ H_B = B \sum_{uv \in E} W_{uv} \sum_{j \in [N]} x_{u,j} x_{u,j+1} \]
となります。
エネルギー関数の最小化により問題が解けるのは何故か #
先ほど定義したエネルギー関数の最小化は、各項について以下のような制約を課しています。
まず、第1項の \(H_A\) の部分は得られるバイナリ変数がハミルトンサイクルをなしているための条件です。 これが0であることで、少なくともハミルトンサイクルであることが満たされます。
次に、第2項の \(H_B\) についてです。 これはハミルトンサイクルの重みの総和を \(B\) 倍した値であることに注意しましょう。 各辺 \(uv \in E\) について、ある \(j \in [N]\) が存在して \(x_{u,j} = x_{v,j+1}=1\) になるときにのみ辺 \(uv\) はハミルトンサイクル上にありますから、そのときにのみ重み \(W_{uv}\) を加えるのです。 すると、これを最小化することは、サイクル上の辺の重みの総和を最小化していることになります。
したがって、エネルギー関数最小化により、ハミルトンサイクルでありながら、重みの総和が最小のものが見つかり、巡回セールスマン問題が解けることになるのです。
もちろん、 \(A\) と \(B\) の大小関係は、ハミルトンサイクルであることが最優先の条件ですから、 \(A > Bmax(W_{uv})\) でなくてはならないことに注意しましょう。
参考文献 #
A. Lucas, “Ising formulations of many NP problems” (open access)