このページでは集合パッキング問題というNP困難な問題をイジングモデルに定式化する方法について述べます。 また、集合パッキング問題がグラフ理論の重要な問題である最大独立集合問題(MIS)と全く同一の問題に帰着されることも述べます。
問題の定式化 #
集合パッキング問題とは、以下のような問題です。 \(n\) 点集合 \(U = \{ 1, 2, \cdots, n\}\) と、その \(N\) 個の部分集合 \(V_i \subseteq U\) が与えられます。 ただし、 \(V_i\) は \(U\) を被覆しているとします。 すなわち、 \[ U = \cup_{i=1}^N V_i \] であるとします。 この時、互いに交わりを持たない \(\{ V_i \}\) の要素からなる部分集合 \(R \subseteq \{ V_i \}\) であって、要素数最大のものは何でしょうか?
この最適化問題はNP困難な問題として知られています。
問題の具体例 #
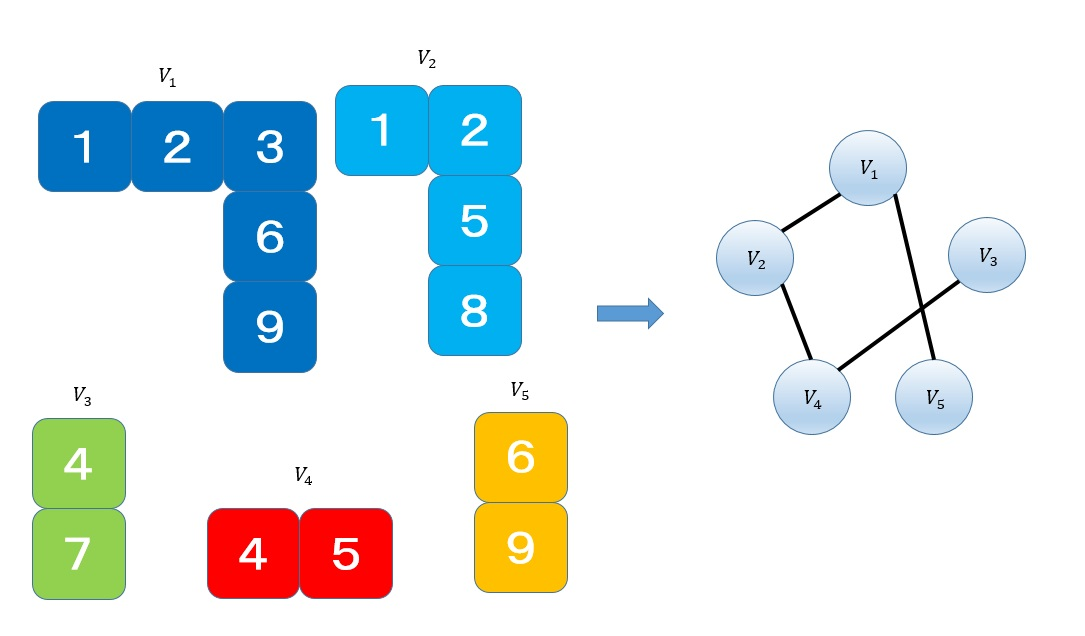
集合 \(U=\{1,2,3,4,5,6,7,8,9\}\) と部分集合 \(V_1=\{1,2,3,6,9\} ,V_2=\{1,2,5,8\} ,V_3=\{4,7\} ,V_4=\{4,5\} ,V_5=\{6,9\}\) を考えます。下の図に分かりやすく図示しました。このとき、 \(V_2,V_3,V_5\) を選択すると各部分集合は共通の要素を持たず、かつ要素数の最大値3を達成します。
イジングモデルへの変形 #
この問題を解くエネルギー関数は以下のようにして構築されます。
各部分集合 \(V_i\) に対して対応するバイナリ変数 \(x_i\) を導入しておきます。 また、 \(A,B\) を正の定数とします。 するとエネルギー関数は、 \[ H = H_A + H_B = A \sum_{i,j: V_i \cap V_j \neq \emptyset} x_i x_j - B \sum_{i = 1}^N x_i \]
エネルギー関数の最小化により集合パッキング問題が解けるのは何故か #
エネルギー関数を最小化することで本当に集合パッキング問題が解けているのでしょうか? これは以下のようにして確かめることができます。
求めたい \(R\) は、エネルギー関数の最小化によって \(x_i = 1\) となった \(V_i\) を集めてつくるものとします。 そのようにして作った \(R\) が集合パッキング問題の解となっていることを確かめましょう。
まず、エネルギー関数を最小化することによって \(H_A = 0\) となったとします。 この時、互いに交わりを持つ \(V_i\) と \(V_j\) については、 \(x_i\) と \(x_j\) が同時に \(1\) になることはありません。 すなわち、得られる \(R\) は集合パッキング問題の解であるための条件「互いに交わりを持たない \(\{ V_i \}\) の要素からなる部分集合であること」を満たしています。
その上で、 \(H_B\) が最小化されることによって \(R\) の要素数が最大化されます。
以上により、エネルギー関数の最小化によって集合パッキング問題が確かに解けていることがわかりました。 ただし、当然 \(H_A = 0\) という要請は \(H_B\) を最小化したいという要請よりも優先されるべきものですから、定数 \(A, B\) は \(A > B\) を満たすよう適切に取らなくてはいけません。
集合パッキング問題から最大独立集合問題への帰着について #
これまで考えてきた集合パッキング問題は、グラフ理論における重要な問題の一つである最大独立集合問題(Maximal Independent Set、MIS)に帰着できる問題です。
ここで、最大独立集合問題とは以下のようにして定式化される問題です。
無向グラフ \(G = (V, E)\) が与えられます。 \(V\) の部分集合であって、どの2点も隣接しないようなもののうち、要素数最大のものは何でしょうか?
今、集合パッキング問題のインスタンス \(n\) 点集合 \(U = \{ 1, 2, \cdots, n\}\) と、その \(N\) 個の部分集合 \(V_i \subseteq U\) に対して、最大独立集合問題のインスタンスを以下のようにして作ることができます、
各 \(V_i\) に対して頂点 \(i\) を作ります。 辺を \(ij \in E \Leftrightarrow V_i \cap V_j \neq \emptyset\) のようにして張りましょう。先ほどの集合パッキング問題の例題から最大独立集合問題に変換する例を以下に図示します。例えば、先ほどの問題の例では \(V_1\) と \(V_2\) は共通要素として1および2を持つので \(V_1,V_2\) 間に辺が張られます。 そうして得られるグラフ \(G = (V, E)\) について、最大独立集合問題を解くと、明らかに元の集合パッキング問題が解けています。
こうして、集合パッキング問題は容易に最大独立集合問題に帰着されることがわかりました。
参考文献 #
A. Lucas, “Ising formulations of many NP problems” (open access)