このページでは最小帰還辺集合問題と呼ばれるNP完全・NP困難な問題をイジングモデルで表現する方法について述べます。
問題の定式化 #
有向グラフ \(G = (V, E)\) が与えられます。 このとき部分グラフ \((V,E-F)\) が無閉路であるような \(F \subset E\) のうち \(|F|\) が最小のものを求めます。 これはNP困難な問題として知られています。
問題の具体例 #
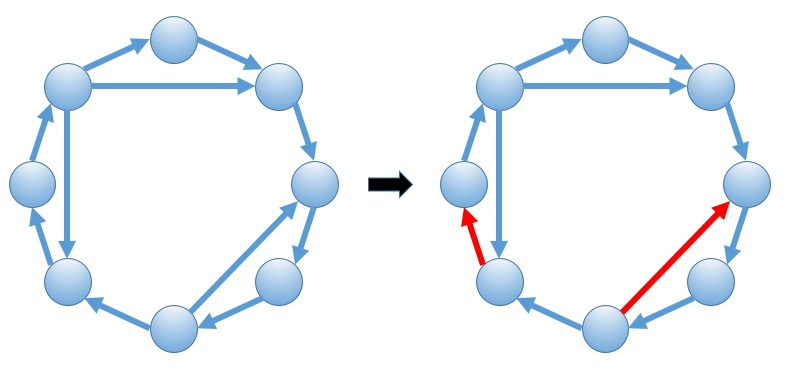
以下のような8個の頂点と11本の有向辺から構成されるグラフを考えます。
このとき、この問題の答えは図の右側の赤い辺の集合で、最小の要素数2を達成します。
実際に、任意の水色の頂点からスタートし元の頂点に戻るような全ての経路について、赤い辺を少なくとも1回通ることが確認できます。このような辺の集合の要素数を最小化する問題です。
イジングモデルへの変形 #
部分グラフ \((V,E-F)\) が無閉路であることは、 辺 \(uv \in E-F\) に対して \(h(u)<h(v)\) であるよう各頂点 \(v \in V\) の高さを決められることと必要十分です。 この考えに則ってエネルギー関数を構成します。
各頂点 \(v\) に対して、 高さが \(i\) であるときに1をとり、そうでないとき0をとるバイナリ変数 \(x_{v,i}\) を定義します。 次に、各辺 \(uv \in E\) に対して、 \(uv \in F\) のとき0をとり、そうでないとき1をとるバイナリ変数 \(y_{uv}\) を定義します。 また、 \(y_{uv}=1\) かつ頂点 \(u\) の高さが \(i\) のとき1をとり、そうでないとき0をとるバイナリ変数 \(x_{uv,i}\) を定義します。
A,Bを正の定数とします。 このとき、エネルギー関数は以下のようになります。 \[ H = H_A + H_B \] \[ H_A = A \sum_{v \in V} \left( 1 - \sum_{i} x_{v,i} \right)^2 + A \sum_{uv \in E} \left( y_{uv} - \sum_{i} x_{uv,i} \right)^2 + A \sum_{uv} \sum_{i} x_{uv,i} \left( 2 - x_{u,i} - \sum_{j>i} x_{v,j} \right) \] \[ H_B = B \sum_{uv \in E} (1 - y_{uv}) \]
エネルギー関数の最小化により問題が解けるのは何故か #
それぞれのエネルギー関数の各項はどのような制約を課しているでしょうか?
まず \(H_A\) の第1項は、 各頂点 \(v\) についてただ一つの高さ \(i\) が存在するという制約を課しています。
また、 \(H_A\) の第2項は、 各辺 \(uv\) に対して、 \(uv \in E-F\) ならばただ一つの高さ \(i\) を持ち、そうでないときは高さを持たないという制約を課しています。
最後に、 \(H_A\) の第3項は、 各辺 \(uv\) が高さ \(i\) を持つとき、頂点 \(u\) の高さが \(i\) かつ頂点 \(v\) の高さ \(j\) が \(j>i\) であるという制約を課しています。
以上の制約により、部分グラフ \((V,E-F)\) に対して各頂点 \(v \in V\) の高さを決めることができます。 よって、エネルギー関数の最小化により \((V,E-F)\) が無閉路であるような \(F\) を得ることが出来ます。
\(H_B\) は帰還辺集合の大きさを最小化するためのものです。 \(uv \in F\) なる辺が少ないほどエネルギー関数が小さくなります。 このとき、帰還辺集合の大きさの最小化よりも制約の遵守を優先するので \(B<A\) である必要があります。
参考文献 #
A. Lucas, “Ising formulations of many NP problems” (open access)