このページでは、次数制約付きの最小全域木問題というNP困難な問題をイジングモデルにより表現する方法について述べます。
問題の定式化 #
無向グラフ \(G = (V, E)\) が与えられます。 また各辺 \(uv \in E\) について、コスト \(c_{uv}\) が定まっています。 さらに、正の自然数の定数 \(\Delta\) が与えられます。
このとき、 \(G\) の全ての頂点を含む木 \(T \subseteq G\) であって、 \(T\) のコスト $$ c(T) = \sum_{uv \in E_T} c_{uv} $$ が最小になるようなもので、 \(T\) の各頂点の次数が \(\Delta\) 以下となるような物を求める問題を考えましょう。
問題の具体例 #
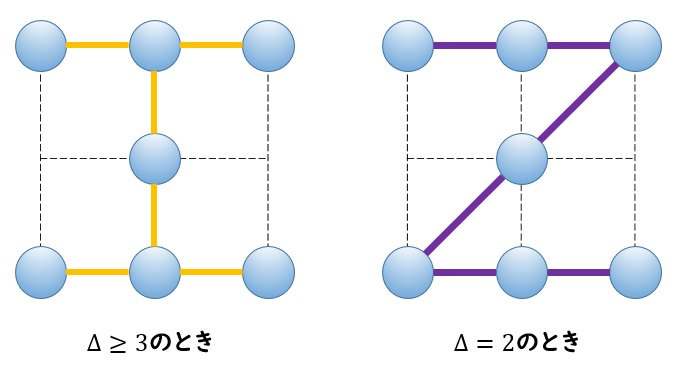
格子点上に7個の頂点が以下の図のような位置関係で存在しています。
このときの最小全域木は図の左側です。
この最小全域木は最大次数が3であるので、
次数制限
\(\Delta\geq3\)
のとき、次数制約付きの最小全域木は図の左側です。
次数制限
\(\Delta=2\)
のとき、次数制約付きの最小全域木は図の右側です。
(
\(\Delta\leq1\)
のときは解がありません。)
イジングモデルへの変形 #
この問題を解くためのイジングモデルのエネルギー関数は以下のようになります。
まず、必要な変数をいくつか導入します。まず、 \(N = |V|\) としましょう。 各辺 \(e \in E\) について、それが \(T\) の辺に含まれるなら1を、そうでないなら0を取るようなバイナリ変数 \(y_e\) を導入します。 また、各頂点 \(v \in V\) と自然数 \(i \in \{ 0, 1, \ldots, N \}\) に対して、頂点 \(v\) が木 \(T\) において根から深さ \(i\) のところにあるときに1を取り、それ以外の時に0を取るようなバイナリ変数 \(x_{v,i}\) を導入します。 また、各辺 \(uv \in E\) と自然数 \(i \in \{ 0, 1, \ldots, N \}\) に対して、木 \(T\) において辺 \(uv\) が根から深さ \(i\) の所に含まれて、かつ \(u\) の方が \(v\) よりも根に近い時に1を、そうでない時に0を取るバイナリ変数 \(x_{uv, i}\) を導入します。 \(x_{uv,i}\) と \(x_{vu,i}\) は別のスピンであることに注意してください。 さらに、各頂点 \(v \in V\) と自然数 \(j \in \{ 1, \ldots, \Delta \}\) に対して、木 \(T\) において頂点 \(v\) の次数が \(k\) の時に \(\sum_{j=1}^\Delta z_{v,j}=k\) となるようなバイナリ変数 \(z_{v,j}\) を導入します。 AとBを正の定数とします。
これらを元にして、エネルギー関数は以下のようになります。 \[ H_{A_1} = A \left( 1 - \sum_{v \in V} x_{v,0} \right)^2 \] \[ H_{A_2} = A \sum_{v \in V} \left( 1 - \sum_{i = 0}^{N/2} x_{v,i} \right)^2 \] \[ H_{A_3} = A \sum_{uv \in E} \left( y_{uv} - \sum_{i=1}^{N/2} (x_{uv,i} + x_{vu,i}) \right)^2 \] \[ H_{A_4} = A \sum_{v \in V} \sum_{i = 1}^{N} \left( x_{v,i} - \sum_{u: uv \in E} x_{uv,i} \right)^2 \] \[ H_{A_5} = A \sum_{v \in V} \left( \sum_{j=1}^\Delta z_{v,j} - \sum_{u: uv \in E} \sum_{i=1}^{N/2} (x_{uv,i} + x_{vu,i}) \right)^2 \] \[ H_{A_6} = A \sum_{uv \in E} \sum_{i=1}^{N/2} x_{uv,i} (2 - x_{u, i-1} - x_{v, i}) \] \[ H_A = H_{A_1} + H_{A_2} + H_{A_3} + H_{A_4} + H_{A_5} + H_{A_6} \] \[ H_B = B \sum_{uv \in E} \sum_{i=1}^{N/2} c_{uv} x_{uv,i} \] \[ H = H_A + H_B \]
エネルギー関数の最小化により問題が解けるのは何故か #
上で定義したエネルギー関数はどのような制約を課しているのでしょうか。
まず、 \(H_{A_1}\) について考えます。 これは、ただ一つの頂点が存在して深さが0となる、すなわち根であるという制約を課しています。
次に、 \(H_{A_2}\) について考えます。 これは各頂点について、ちょうど一つの根からの深さ \(i\) が存在するという制約を課しています。
次に、 \(H_{A_3}\) について考えます。 これは各辺について、その辺を木 \(T\) が含む時に、ある一つの根からの深さ \(i\) が存在して、その辺がちょうど深さ \(i \) の位置にあるという制約を課しています。
次に、 \(H_{A_4}\) について考えます。 これは各頂点 \(v\) と根からの各深さ \(i\) について、その頂点が木においてその深さを持つ時に、ちょうど一つの \(v\) を含む辺 \(uv \in E\) が存在して、その辺が深さ \(i\) を持って、 \(u\) の方が \(v\) よりも根に近いということが成り立つ、という制約を課しています。
次に、 \(H_{A_5}\) について考えます。 これは各頂点 \(v\) について、その頂点が木において次数 \(j\) を持つ時に、その頂点を含む辺のうち木に含まれるものがちょうど \(j\) 本であるという制約を課しています。
次に、 \(H_{A_6}\) について考えます。 これは各辺 \(uv \in \) と根からの各深さ \(i\) に対して、辺 \(uv\) が \(u\) の方が \(v\) よりも根に近く深さ \(i\) の状況で木に含まれているときに、 頂点 \(u\) が木に深さ \(i-1\) で含まれ、頂点 \(v\) が木に深さ \(i\) で含まれるという制約を課しています。
以上の6つの制約により、得られる木が次数制約を満たす全域木であることが保証されます。
最後に、 \(H_B\) について考えます。 これは、得られる木の重さを最小にするためのものです。 実際、これは得られる木の重みの総和になっています。 したがって、これを最小化することで重みを最小化していることになります。
もちろん、次数制約を満たす全域木であることは、最小性よりも優先する条件ですから、 \(A > Bmax(c_{uv})\) でなくてはいけません。
参考文献 #
A. Lucas, “Ising formulations of many NP problems” (open access)