このページでは、整数長ジョブスケジューリング問題と呼ばれるNP困難な問題をイジングモデルで表現する方法について述べます。
問題の定式化 #
\(N\) 個のジョブと、 \(m\) 個のコンピュータがあります。 各ジョブ \(i\) は長さ \(L_i\) を持っていて、どれかのコンピュータにアサインしたいとします。 コンピュータ \(\alpha\) にアサインされるジョブの集合を \(V_\alpha\) としたとき、そのコンピュータにアサインされるジョブの長さの合計 \(M_\alpha = \sum_{i \in V_\alpha} L_i\) の最大値 \(\max M_\alpha\) を最小化するようなジョブのスケジューリングは何でしょうか?
この問題はNP困難な問題として知られています。
問題の具体例 #
\(N=7\)
個のジョブがあり、
\(m=3\)
個のコンピュータがあります。各ジョブの長さは
\(L_1=7,L_2=5,L_3=3,L_4=2,L_5=2,L_6=2,L_7=2\)
です。ここで、
\(V_1=\{2,3\},V_2=\{4,5,6,7\},V_3=\{1\}\)
とすると
\(M_1=8,M_2=8,M_3=7\)
であり、
\(\max (M_1,M_2,M_3)=8\)
となります。これがこの問題の最適解になります。
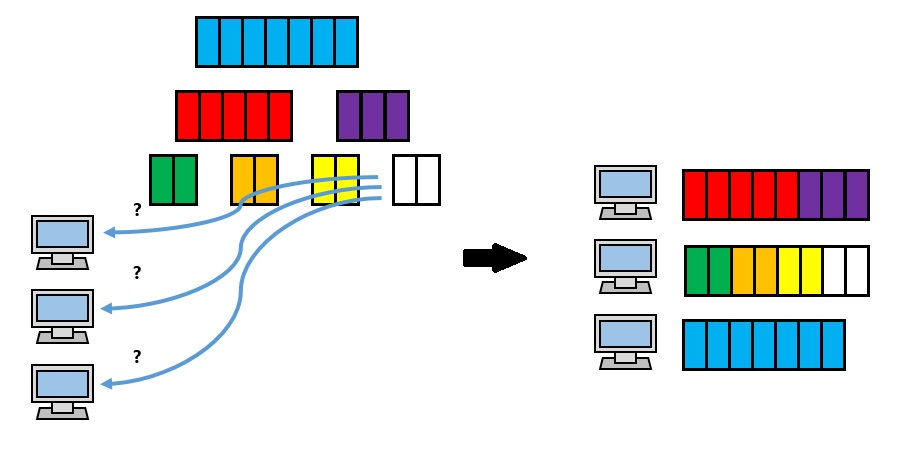
イジングモデルへの変形 #
この問題を解くイジングモデルのエネルギー関数は以下のように構築されます。
まず、一般性を失わずに任意の \(\alpha\) に対して、 \(M_1 \ge M_\alpha\) と仮定できることに注意します。 各ジョブ \(i\) と、各コンピュータ \(\alpha\) に対してバイナリ変数 \(x_{i, \alpha} \in \{ 0,1 \}\) を設定します。 これは、ジョブ \(i\) がコンピュータ \(\alpha\) にアサインされる時に1をとり、そうでないときに0を取ります。 また、1以外の \(\alpha\) と0以上の自然数 \(n\) に対してバイナリ変数 \(y_{i, \alpha} \in \{ 0,1 \}\) を設定します。 これは、 \(M_1 - M_\alpha = n\) の時に1を取り、それ以外の時に0を取ります。 また、 \(A\) と \(B\) を正の定数とします。 さらに、 \(M\) をユーザが定める正の定数とします。(決め方はあとで述べます。) この時エネルギー関数は以下のようになります。
\[ H = A\sum_{i \in [N]} \left( 1 - \sum_{\alpha \in [m]} x_{i,\alpha} \right) ^2 + A \sum_{\alpha \in [m]} \left( \sum_{n \in [M]} n y_{n,\alpha} + \sum_{i \in [N]} L_i (x_{i,\alpha} - x_{i, 1} )\right)^2 + B \sum_{i \in [N]} L_i x_{i,1} \]エネルギー関数の最小化により問題が解けるのは何故か #
先ほど定義したエネルギー関数の最小化は、各項について以下のような制約を課しています。
第1項は、各ジョブについてそれを実行するコンピュータがちょうど一つであるという制約を課しています。
第2項は、各コンピュータ \(\alpha\) において割り当てられるジョブの長さの合計がコンピュータ1に割り当てられるジョブの長さを超えないという制約を課します。 厳密にはさらに強く、 \(M_1 - M_\alpha = n\) であるということを課しています。
第3項は、最大の長さ \(M_1\) を最小にするための制約です。ここで、長さの最小化よりも制約を守ることを優先するので \(A>Bmax(L_{i})\) である必要があります。
正定数 \(M\) とは何か #
\(M\) は、各コンピュータに割り当てられるジョブの長さが最大の物 \(M_1\) に比べてどの程度変わりうるかを表した数です。 したがって、最悪の場合 \(M\) は \(N\max L_i\) となります。 現実的には、考えうるジョブの長さの大小を考慮して適切に選ぶことになります。
参考文献 #
A. Lucas, “Ising formulations of many NP problems” (open access)