このページでは、グラフ彩色問題と呼ばれるNP完全な問題をイジングモデルで表現する方法について述べます。
問題の定式化 #
無向グラフ \(G = (V, E)\) と、 \(n\) 個の色の集合が与えられます。 \(G\) の頂点は隣り合う頂点が同じ色にならないように \(n\) 色で塗り分けることができるでしょうか?
問題の具体例 #
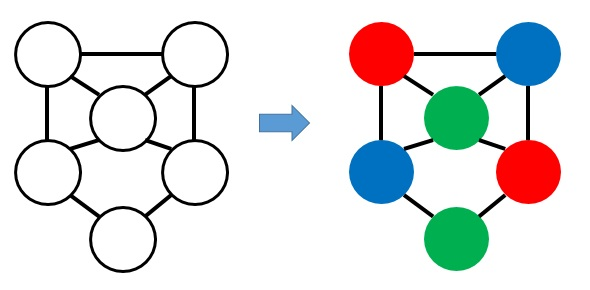
図のようなグラフを3色で塗り分ける問題を考えます。図の右側のようにグラフを彩色したとき、隣り合う頂点同士は違う色になっていることが分かります。よってこの問題の答えはYESです。
イジングモデルへの変形 #
この問題を解くイジングモデルのエネルギー関数は以下のように構築されます。
まず、各頂点 \(v \in V\) と各色 \(i \in [n]\) に対して、 頂点 \(v\) が色 \(i\) に塗られたとき1をとり、そうでないとき0をとるバイナリ変数 \(x_{v,i} \in \{ 0, 1\}\) を導入しておきます。 \(A\) を正の定数として、エネルギー関数は以下のように表せます。 \[ H = A\sum_{v \in V} \left( 1 - \sum_{i \in [n]}x_{v,i} \right)^2 + A \sum_{uv \in E}\sum_{i \in [n]} x_{u,i} x_{v,i} \]
エネルギー関数の最小化によりグラフ彩色問題が解けるのは何故か #
先ほど定義したエネルギー関数の最小化は、各項について以下のような制約を課しています。
まず、第1項は、各頂点 \(v \in V\) についてちょうど一つの色のみが使われているという制約を課しています。
次に第2項は、各辺 \(uv \in E\) についてその両方の端点に同じ色が使われないという制約を課しています。
参考文献 #
A. Lucas, “Ising formulations of many NP problems” (open access)