このページでは、ナップサック問題と呼ばれるNP困難な問題をイジングモデルで表現し解く方法について述べます。 この問題は参考文献1において「不等式付き問題(Problems with Inequalities)」に分類されている問題です。 このタイプの問題はイジングモデルとして定式化し、そのエネルギー関数を量子アニーリングマシンに埋め込む際に、連結度の高いグラフを必要とします。 そのため、現在のハードウェアでは十分に解くことができないタイプの問題であることに注意してください。
問題の定式化 #
\(N\) 個の物 \(\{ 1, \ldots, N\}\) があり、一つ一つが \(\alpha\) で添え字付けされています。 一つ一つの \(\alpha \in \{1 , \ldots, N\}\) の重さは \(w_\alpha\) で与えられ、価値は \(c_\alpha\) で与えられるとしましょう。 このとき、幾つかの物をかばん(knapsack)の中に入れていくことにします。 ただし、かばんの重さは \(W\) を超えてはいけません。 このとき、かばんに入れる物の価値の総和を最大にするような入れ方はなんでしょうか?
より厳密にいえば、以下のようになります。 \(x_\alpha\) を、物 \(\alpha\) をかばんに入れるとき1をとり、かばんに入れないとき0をとるバイナリ変数だとします。 すると、かばんに入っている物の重さの合計は \[ \mathcal{W} = \sum_{\alpha=1}^N w_\alpha x_\alpha \] となり、かばんに入っている物の価値の合計は \[ \mathcal{C} = \sum_{\alpha=1}^N c_\alpha x_\alpha \] となります。 この時、 \(\mathcal{W} \le W\) のもとで \(\mathcal{C}\) を最大化する \(\{ x_\alpha \}\) を求めてください。
ただし、ここでは各重み \(w_\alpha\) や価値 \(c_\alpha\) は整数であるとします。
問題の具体例 #
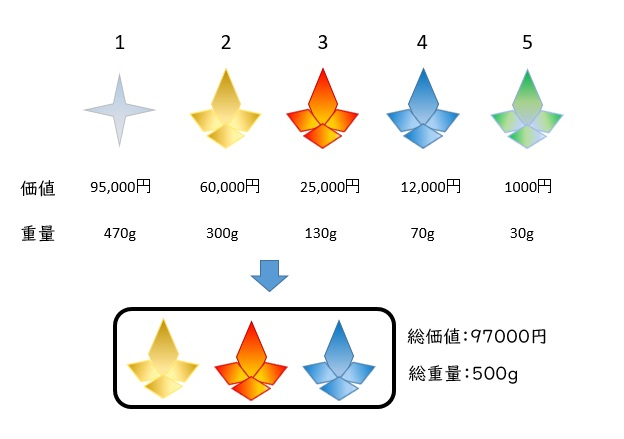
以下の図のような5個の宝石があります。
かばんの制限重量が
\(W=500(g)\)
であるとき、持って帰ることのできる宝石の総価値を最大化することを考えます。
宝石2、宝石3、宝石4を選ぶと総重量
\(500(g)\)
と制限容量を満たした上で総価値が97000円となり、このときがこの問題の最適解になります。
イジングモデルへの変形 #
この問題を解くイジングモデルのエネルギー関数は以下のようにして作ることができます。
まず、各 \(n \in \{ 1, \ldots, W\}\) に対して、 \(y_n\) をかばんの重さが \(n\) であるかどうかを表すバイナリ変数としましょう。 また、 \(A,B\) を正の定数としましょう。 するとエネルギー関数は以下で与えられます。 \[ H = H_A + H_B \] \[ H_A = A \left( 1 - \sum_{n=1}^W y_n \right)^2 + A\left( \sum_{n=1}^W n y_n - \sum_{\alpha=1}^N w_\alpha x_\alpha \right)^2 \] \[ H_B = -B\sum_{\alpha = 1}^N c_\alpha x_\alpha \]
エネルギー関数の最小化により整数重みナップサック問題が解けるのは何故か #
ここでは、上で定義したエネルギー関数を最小化することで、整数重みナップサック問題が解ける理由を説明します。
まず、エネルギー関数の最小化により \(H_A = 0\) となったとしましょう。 このとき、第1項が0でであることから、ただ一つの \(n \in \{ 1, \ldots, W \}\) に対して \(y_n = 1\) となっています。 さらに第2項が0であることより、その \(n\) とかばん内の物の重さの合計が等しいことがわかります。
また、 \(H_B\) が最小化されることにより、かばん内の物の価値の合計が最大化されることになります。
したがって、エネルギー関数の最小化により整数重みナップサック問題が解けることになります。
おまけ #
- エネルギー関数の最小化において、 \(H_A\) の最小化は \(H_B\) の最小化よりも優先します。 したがって、正定数は \(B \max c_\alpha < A\) となるように取らなくてはいけません。 ( \(B\) ではなく \(B \max c_\alpha\) となっているのは、たった一つでかばんの重さ制約を破壊してしまう物を許さないためのものです。)
また、必要なスピン数は \(N + \lfloor 1 + \log W \rfloor\) です。