このページでは、クリークカバー問題と呼ばれるNP完全な問題をイジングモデルで表現する方法について述べます。
問題の定式化 #
無向グラフ \(G = (V, E)\) と、 \(n\) 個の要素からなる色の集合が与えられます。 \(G\) の各頂点を \(n\) 種類の色で塗っていきます。 \(W_1, W_2, \ldots, W_n\) を頂点集合 \(V\) の部分集合たちであって、各色 \(1, 2, \ldots, n\) で塗られたものとしましょう。 また、 \(E_{W_1}, E_{W_2}, \ldots , E_{W_n}\) を辺集合 \(E\) の部分集合たちであって、各 \(W_i\) 内の頂点どうしを結んだ辺のみに制限したものとします。 このとき、全てのグラフ \((W_i, E_{W_i})\) が完全グラフになる(クリークをなす)ようにできるでしょうか?
問題の具体例 #
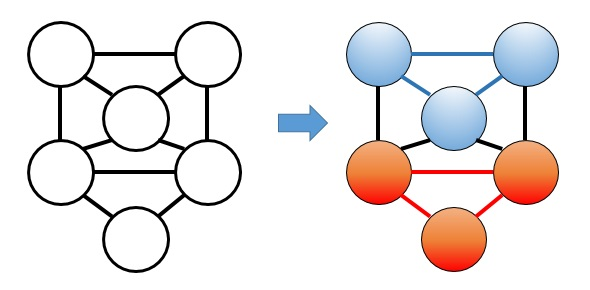
以下の図のようなグラフを2色に塗り分けることを考えます。
図の右側のようにグラフを彩色すると、水色の頂点同士は互いをつなぐ辺を持っていることが分かります。赤色の頂点同士も同様です。
よってこの問題の答えはYESです。
イジングモデルへの変形 #
この問題を解くイジングモデルのエネルギー関数は以下のように構築されます。
まず、各頂点 \(v \in V\) と各色 \(i \in [n]\) に対して、 頂点 \(v\) が色 \(i\) に塗られたとき1をとり、そうでないとき0をとるバイナリ変数 \(x_{v,i} \in \{ 0, 1\}\) を導入しておきます。 \(A, B\) を正の定数として、エネルギー関数は以下のようになります。
\[ H = A\sum_{v \in V} \left( 1 - \sum_{i \in [n]}x_{v,i} \right)^2 + B \sum_{i \in [n]} \left[ \frac{1}{2} \left( -1 + \sum_{v \in V} x_{v,i}\right)\sum_{v \in V}x_{v,i} - \sum_{uv \in E} x_{u,i} x_{v,i} \right] \]エネルギー関数の最小化によりなぜ問題が解けるのか #
先ほど定義したエネルギー関数の最小化は、各項について以下のような制約を課しています。
第1項は各頂点についてちょうど一つの色が使われるという制約を課しています。
第2項について考えましょう。 まず、色 \(i\) に対して、全ての頂点にわたる和 \(\sum_{v \in V}x_{v,i}\) は色 \(i\) が使われた頂点の数 \(|W_i|\) を表すことに注意します。 すると、グラフ \((W_i, E_{W_i})\) がクリークをなしているとすれば、その辺数は \(W_i\) の中から2個選ぶ場合の数に等しく、 \[ \frac{1}{2}|W_i| (|W_i| - 1) = \frac{1}{2} \left( -1 + \sum_{v \in V} x_{v,i}\right)\sum_{v \in V}x_{v,i} \] となり、第2項の \(i\) に関する和の内部の1項目が得られます。 我々は、これがグラフ \((W_i, E_{W_i})\) の辺数に等しいという制約を課したいので、これからグラフ \((W_i, E_{W_i})\) の辺数 \(\sum_{uv \in E} x_{u,i} x_{v,i}\) を引き算してあげます。 この引き算する値の最大値が、和の内部の1項目ですから、もちろんこれは全体として非負であって、正の時に制約が破られペナルティが課されることになります。
参考文献 #
A. Lucas, “Ising formulations of many NP problems” (open access)