このページではグラフ同型問題と呼ばれる問題をイジングモデルで表現する方法について述べます。
問題の定式化 #
グラフ同型問題とは、 グラフ \(G_{1} = (V_{1}, E_{1})\) およびグラフ \(G_{2} = (V_{2}, E_{2})\) が与えられたときに、 \(G_{1}\) と \(G_{2}\) が同型かを判定する問題です。
\(G_{1}\) と \(G_{2}\) が同型であるとは、 \(G_{1}\) の任意の2頂点 \(u,v \in V_{1}\) に対して、 \((u,v) \in E_{1}\) となるのが \((f(u),f(v))\in E_{2}\) となるとき、かつその時に限るような \(V_{1}\) から \(V_{2}\) への全単射写像 \(f\) が存在することを言います。
この問題をイジングモデルで表現するにあたり、 \(G_{1}\) の隣接行列 \(A_{1}\) と \(G_{2}\) の隣接行列 \(A_{2}\) について、 \(A_{2}=P^{T}A_{1}P\) である置換行列 \(P\) が存在するかを判定します。 このような \(P\) が存在するとき \(G_{1}\) と \(G_{2}\) は同型です。
この問題はNPに属することは分かっていますが、Pに属するのかNP完全に属するのか、もしくは他のクラスに属するのか分かっていません。 しかし、困難な問題であるとは言われています。
問題の具体例 #
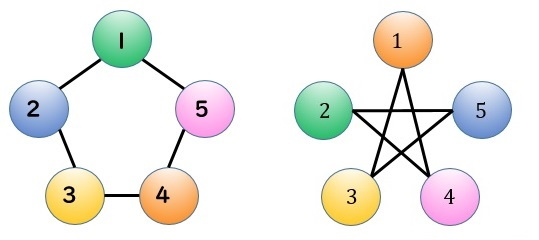
以下のような二つのグラフを考えます。
以下の二つのグラフは頂点の番号に注目すると隣接行列が異なりますが、色に注目すると隣接行列が一致します。
例えば、どちらのグラフもオレンジの頂点は黄色の頂点とピンクの頂点と隣接関係にあり、他の頂点とは隣接関係にありません。
よって、この2つのグラフは同型です。
イジングモデルへの変形 #
グラフが同型であるのは \(|V_{1}|=|V_{2}|\) であるときに限るので、以下ではこれを前提に考えます。
頂点 \(v \in V_2\) が頂点 \(i \in V_{1}\) に写像されるとき1をとり、そうでないとき0をとるバイナリ変数 \(x_{v,i}\) を定義します。
A,Bを正の定数とします。 このとき、エネルギー関数は以下のようになります。
\[ H = H_A + H_B \] \[ H_A = A \sum_{v \in V_{2}} \left( 1- \sum_{i \in V_{1}} x_{v,i} \right)^2+ A \sum_{i \in V_{1}} \left( 1 - \sum_{v \in V_{2}} x_{v,i} \right)^2 \] \[ H_B = B \sum_{ij \notin E_1} \sum_{uv \in E_2} x_{u,i} x_{v,j}+ B \sum_{ij \in E_1} \sum_{uv \notin E_2} x_{u,i} x_{v,j} \]
エネルギー関数の最小化により問題が解けるのは何故か #
それぞれのエネルギー関数の各項はどのような制約を課しているでしょうか?
まず \(H_A\) は写像が全単射であるであるという制約を表しています。 各頂点 \(v \in V_2\) が頂点 \(i \in V_{1}\) と一対一に対応するとき \(H_A=0\) になります。
また、 \(H_B\) はグラフの接続関係が正しいという制約を表しています。 写像した結果もともと繋がっていない辺が繋がってしまったり、もともと繋がっていた辺が繋がらなくなった場合にペナルティーを課します。
基底状態が \(H=0\) とき、この二つのグラフは同型であると判断できます。
参考文献 #
A. Lucas, “Ising formulations of many NP problems” (open access)