このページでは、ハミルトンパス問題及びハミルトンサイクル問題と呼ばれるNP完全な問題をイジングモデルで表現する方法について述べます。
問題の定式化 #
無向でも有向でも良いグラフ \(G = (V, E)\) があります。 また、 \(V\) の頂点は \(1, 2, \ldots, N\) とラベルづけされているとします。
ハミルトンパス問題とは、ある頂点から出発して \(G\) の辺だけを使って二度と同じ頂点を踏まないように全ての頂点を1回ずつ通る経路(パス)は存在するかという問題です。
一方で、ハミルトンサイクル問題とは、ある頂点から出発して \(G\) の辺だけを使って二度と同じ頂点を踏まないように全ての頂点を1回ずつ通り、最後に出発した頂点に戻ってくるようなサイクルは存在するかという問題です。
これらは共にNP完全な問題として知られています。
問題の具体例 #
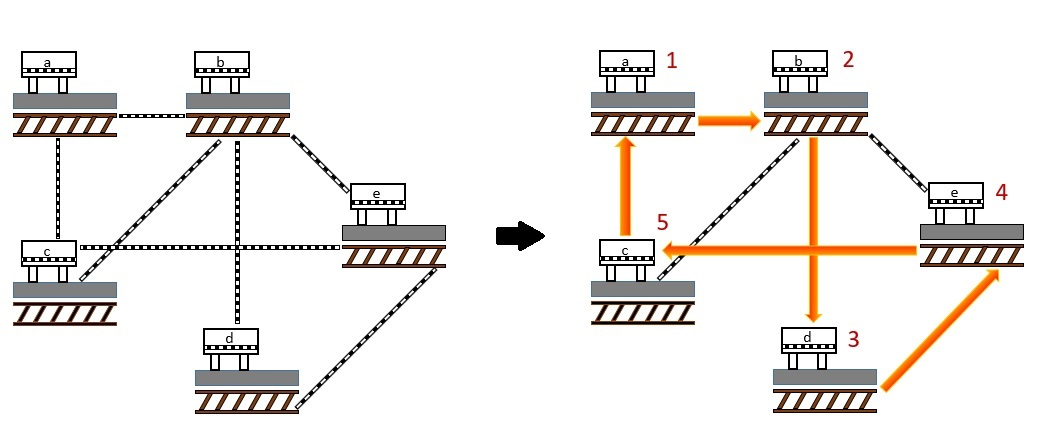
例題としてハミルトンサイクル問題を考えてみましょう。以下の図のような5つの駅と路線があります。駅
\(a\)
から出発して、駅
\(b,c,d,e\)
を一度ずつ通って駅
\(a\)
に戻ってくる経路は存在するでしょうか。答えはYESです。図の右側のような
\(a→b→d→e→c→a\)
という経路が条件を満たします。
イジングモデルへの変形 #
ハミルトンサイクル問題に関するイジングモデルへの変形についてまずは述べましょう。 ハミルトンパス問題は、ハミルトンサイクル問題が解ければサイクルの最後の1辺を無視すれば解が得られますから、ハミルトンサイクル問題が解ければ十分です。
また、グラフは一般性を失わずに有向グラフであると仮定できます。 無向グラフが与えられた場合は、各辺に対して両方向の有向辺を与えれば良いからです。
各頂点 \(v\) と、サイクルにおける順番 \(i\) に対して、 \(v\) がサイクルの \(i\) 番目であるときに1をとり、そうでないときに0を取るバイナリ変数 \(x_{v,i}\) を用意しましょう。 また、 \(A\) は正の定数とします。 このときエネルギー関数は以下のようになります。
\[ H = A \sum_{v \in [N]} \left( 1 - \sum_{j \in [N]} x_{v,j} \right)^2 + A \sum_{j \in [N]} \left( 1 - \sum_{v \in [N]} x_{v,j} \right)^2 + A \sum_{uv \not\in E} \sum_{ j \in [N]} x_{u,j} x_{v,j+1} \]エネルギー関数の最小化により問題が解けるのは何故か #
先ほど定義したエネルギー関数の最小化は、各項について以下のような制約を課しています。
第1項は、各頂点 \(v \in [N]\) についてそれがサイクルの中の何番目であるかはただ一つに定まるという制約です。
第2項は、逆にサイクルの中の順番 \(j \in [N]\) について \(j\) 番目の頂点はただ一つしかないという制約です。
第3項は、ハミルトンサイクルは \(G\) の辺 \(E\) だけからできているはずですから、 \(E\) の元ではない \(uv\) に対して、何らかの順番 \(j\) が存在して、 \(u\) が \(j\) 番目であり \(v\) が \(j+1\) 番目であるという状況はあってはなりませんから、これにペナルティを課します。
このような制約を満たすように作られた \(\{ x_{v,i} \} \) は、確かにハミルトンサイクルを表すことが容易にわかります。
参考文献 #
A. Lucas, “Ising formulations of many NP problems” (open access)