アニーリングマシンのプログラミングでは、定式化された最適化問題をアニーリングマシン上で実行するまでの流れについて説明しました。このページでは実際に量子アニーリングマシンを利用して問題を解く例として、「データクラスタリング」を取り上げて説明します。
クラスタリングとは #
クラスタリングとは、分類対象の集合をクラスタと呼ばれる部分集合に分割する手法です。多数のデータが与えられた時に「同じクラスタ内の対象は互いに似ている」「違うクラスタにある対象は似ていない」という分類を行います。基本的なデータ解析手法の1つであり、データマイニングや統計分析などで利用されます。
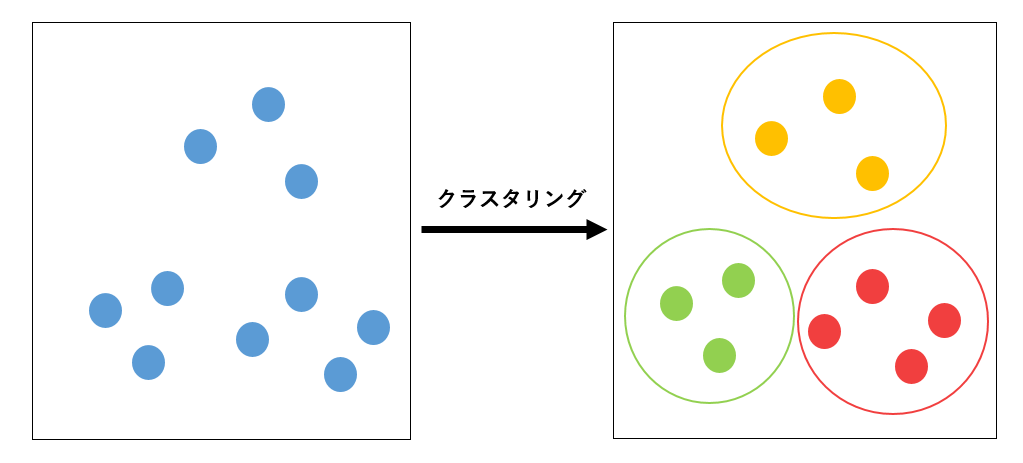
2次元平面上の点の分類 #
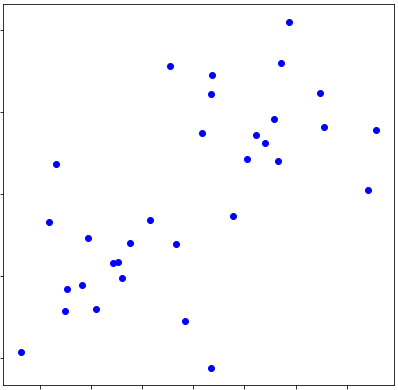
最も典型的な例として、上の図のように2次元平面上の多数の点を、距離が近いもの同士で分類するクラスタリングをアニーリングマシンを用いて行います。
最適化問題を実際にアニーリングマシンを用いて解く為には、問題を QUBO やイジング形式によって表現する必要があります。そのため、まずはクラスタリングをエネルギー関数で表現するところから考えます。
QUBO によるエネルギー式 #
クラスタリング対象の点1つ1つにとって、望ましくない「コスト」を考えると、同じクラスタに所属する点同士の「距離」が対応すると考えるのが自然です。そのため最もシンプルなクラスタリングのコストとして下記の式で表すことにします。
\[ H_{\mathbf{cost}} = \sum_{k}\sum_{i \ne j}{d_{ij} q_{ik} q_{jk}} \]ここで、 \(i,j\) は点のインデックスを、 \(d_{ij} \ge 0\) は点 \(i,j\) 間の距離を表します。 \(q_{ik}\) は QUBO 変数として、点 \(i\) に対しクラスタ \(k\) に所属する場合に \( 1 \) 、そうでない場合に \(0\) を取ることにします。つまりこの式は、全クラスタに対して所属する全ての点の間の距離を足し合わせたものを表します。これをグラフで表現すると3点2クラスタについて下記の図のようになります。
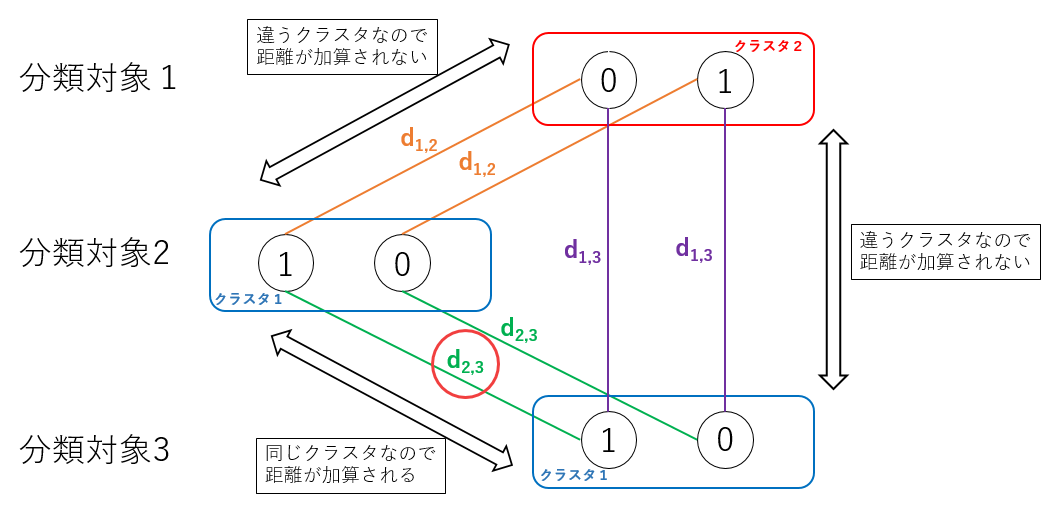
所属クラスタのビット表現 #
上の式では点 \(i\) の所属クラスタについて \(k\) ビットで表現されています。よって、 \( N \) 点を \( K \) クラスタに分類する場合には \( N K\) ビット必要になります。
実はこの式はこのままでは不十分です。なぜなら、 \(H_{\mathbf{cost}}\) の最小値は考えるまでもなく \(q_{ik} = 0\) 、つまりすべての点がどのクラスタにも所属していない状態になってしまいます。そのためすべての点に対して、どれか1つのクラスタに所属するという「制約条件」をかける必要があります。
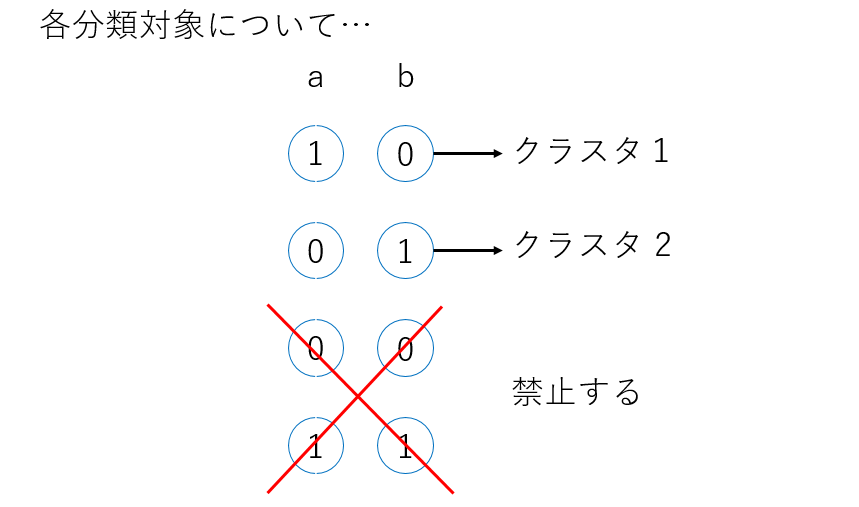
例えば \(a,b\) 2つのクラスタがある場合、所属クラスタを表す \(2\) ビットは上の図のように必ず片方だけ1を取るようにします。結論だけ書くと、下記のようなペナルティ項を各点に対して強く与えることで実現できます。
\[ {H_p}^i = c_i \left( q_{a}q_{b}-(q_{a}+q_{b})/2 \right) \]ここで \(c \ge 0\) は適当な定数です。制約を守るために必要な大きさは \(d_{ij}\) に依存します。この式は \(q_a = q_b = 0\) と \(q_a = q_b = 1\) に対して 0 より大きい値を取るために、必ずどれか一つのクラスタに所属することを表すペナルティとして機能します。
以上の考え方を \(K\) 個のクラスタに対しても同様の式を立てることで一般化し、全体の QUBO 式として、
\[ H = \sum_{k}\sum_{i \ne j}{d_{ij} q_{ik} q_{jk}} + \sum_i{{H_p}^i} \]という形が今回の問題設定におけるクラスタリングの QUBO 式となります。
アニーリングマシンによる最適化 #
今回はアニーリングマシンとして D-Wave の量子アニーリングマシン D-Wave 2000Q と、半導体による富士通デジタルアニーラを用いました。それぞれ 2048ビット疎結合、1024ビット全結合を持つマシンですが、今回の QUBO 式はほとんど全てののビット間の結合を要求するため、最大で D-Wave マシンでは 64 ビット、富士通マシンでは 1024 ビットの規模の問題に対して実行しました。
2クラスタ分類 #
まず最も簡単な 2クラスタの分類を行います。D-Wave マシンについては \( 64 / 2 = 32 \) より、32点について実行しました。
分類前は下記の散布図で表されています。
クラスタリング前 #
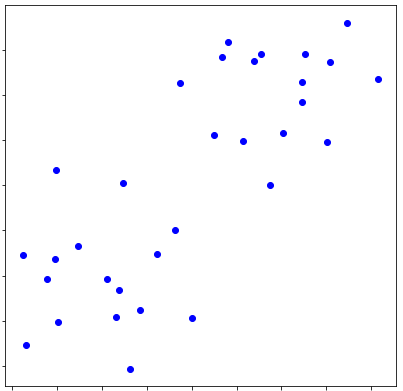各点の間の距離を用いて QUBO 式を組み立て D-Wave マシンの結果で塗り分けると以下のようになりました。
クラスタリング後 #
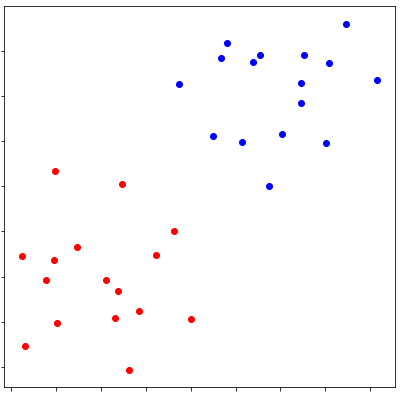確かに距離が近いもの同士で正しく塗りわけられているように見えます。
一方、富士通デジタルアニーラではより大きな問題となる 512 ( \( = 1024 / 2\) )点の分類を実行しました。
クラスタリング前 #
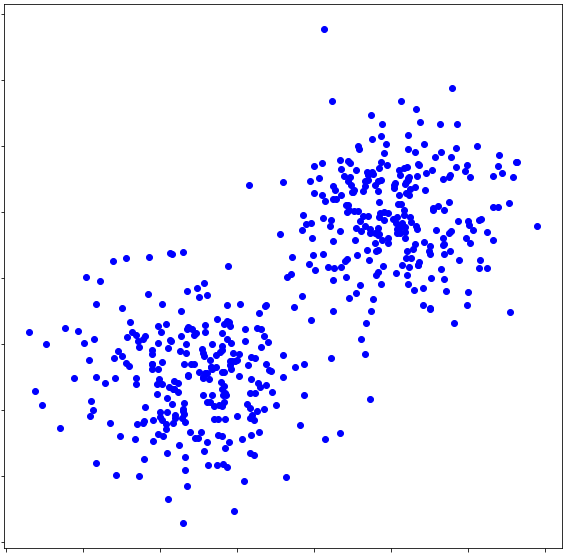
クラスタリング後 #
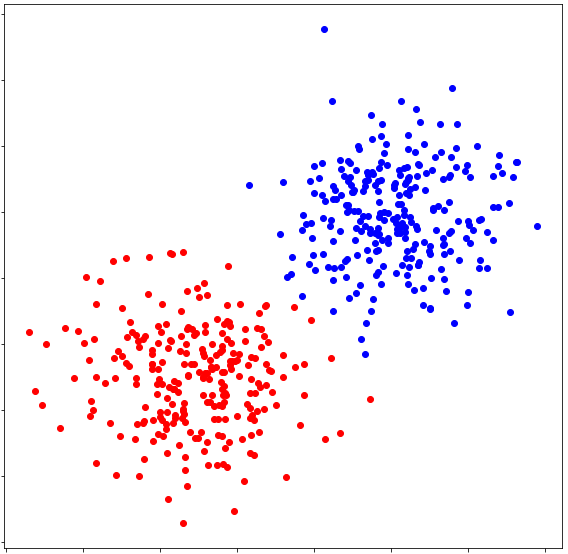こちらも正しくクラスタリング出来ているように見えます。
多数クラスタへの分類 #
より多くのクラスタについても クラスタ数について一般化された QUBO 式を用いることで実行できます。ただしクラスタ数の増加に対して必要ビット数が比例するため、実行できる点の数は減少します。
下記は 富士通デジタルアニーラによる3～6クラスタへの分類です。
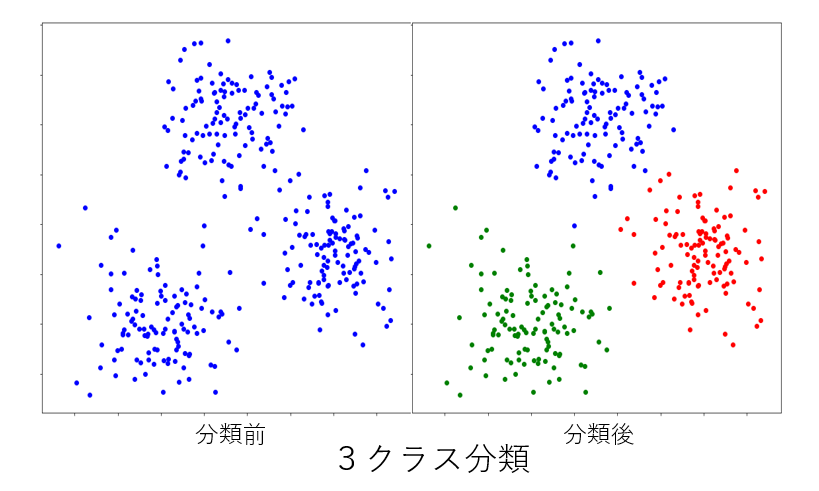
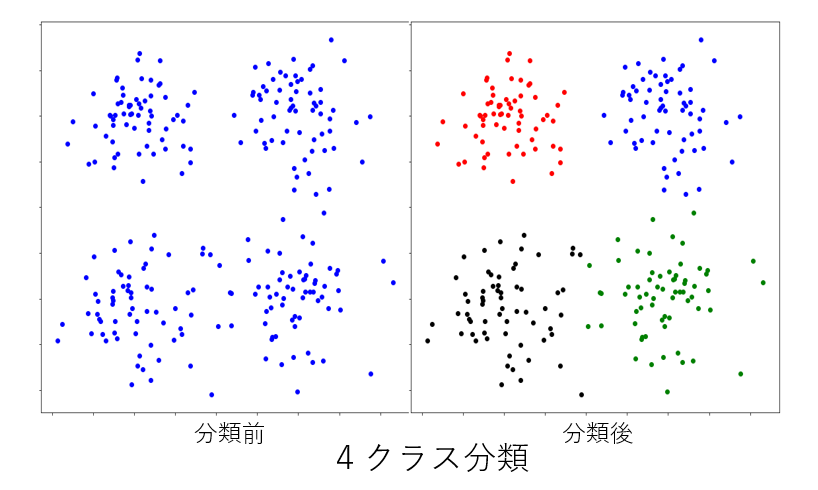
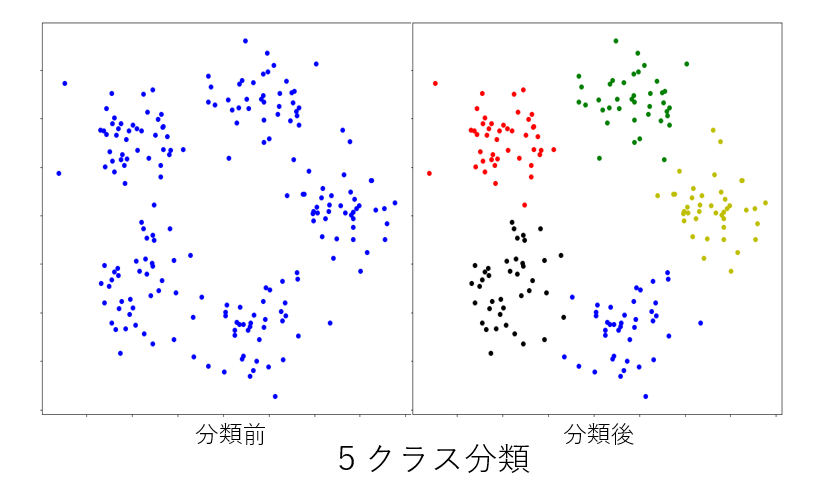
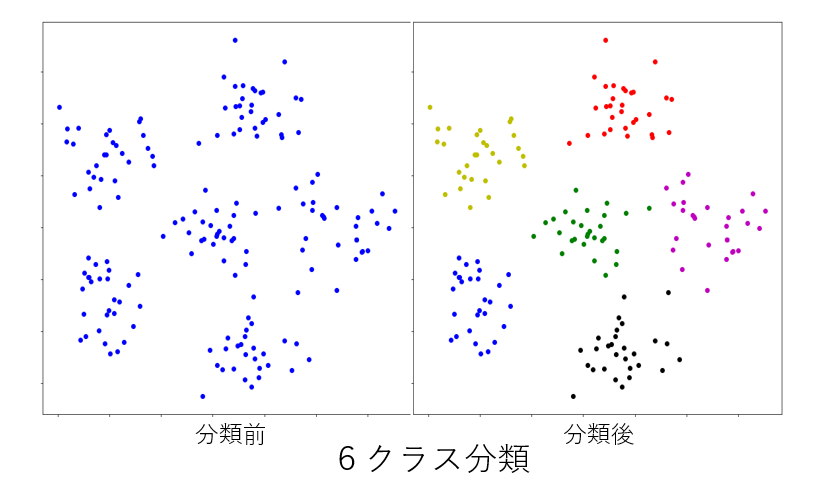
最後に #
今回扱った問題は二次元平面上の点の間のユークリッド距離を利用していましたが、物理的な距離に限らず、分類対象同士の間で何らかの距離的な概念を定義することさえ出来れば、同様の手法でクラスタリングを行うことが出来ます。
この手法の利点は、コスト関数をベースに組合せ最適化処理を行うため、例えばk平均法で生じるような最適解の初期値依存が (同じヒューリスティクスとしても) 比較的小さいということが挙げられます。
また今回は説明の簡便さから非常にシンプルなコスト関数の QUBO 表現を用いました。実は今回の式には致命的な問題があり、クラスタに含まれるの点の数が同一に近くなるような作用が (距離コストより) 強く生じます。これはクラスタに含まれる点の間の距離を単純に足し合わせているために、クラスタ内の足し合わせる数が2乗で大きくなってしまうからです。
上記の問題点を踏まえ、発展問題としてクラスタの重心位置や平均の距離を用いたコスト関数への改修や、アルゴリズムの改良などが考えられます。また既存のクラスタリングアルゴリズムをベースに QUBO 式表現を考えることで、より精度の高いクラスタリングに挑戦してみるのも興味深いと思われます。