解きたい組合せ最適化問題をイジング模型に表現したとしても、マシンによっては変数ノード間で結合が自由に作成できない場合があります。これはマシンがビット配置を非完全グラフで実装しているためです。ここでは非完全グラフ上のイジング模型において、どのようにして任意の変数ノード間で結合を作成するかについて説明します。
複数ノードによるチェイン #
例として、二次元正方格子上に変数ノードが配置されているグラフで実装されたマシンがあったとします。このマシンでは上下左右の結合のみが許されています。そのため、例えば三角格子上のイジング模型はそのままでは埋め込むことが出来ません。
この場合の対処法として、隣接した複数のノードを一つのノードとみなすという方法が使われます。
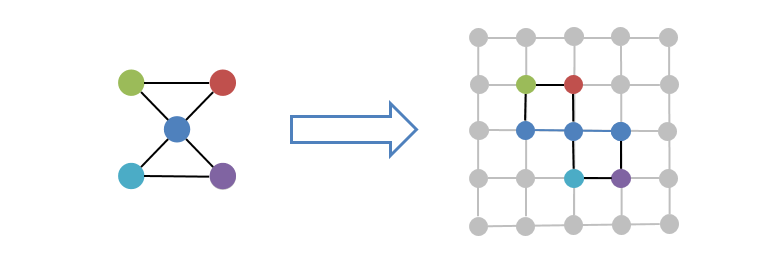
上図において正方格子へのマッピングの一例を図示します。左の三角形の頂点は正方格子上の対応する色の頂点にマッピングされています。左図中央の青いノードはマッピング後、右図の3ノードが担うことになりました。
このように1体多の対応を行うことで、本来は許されない結合が実現できます。ただし対応させた複数ノードは、必ずマッピング後に隣接している必要があります。なぜなら、このマッピングは複数変数を一つの変数としてみなしているからです。複数変数を一つの変数としてみなすためには、制約条件を追加しないといけなくなりますが、それを隣接相互作用という形で実現する必要があります。
具体的にどのような制約を加えればよいかを考えていきます。例えばイジング模型をマシンのグラフにマッピングしてる最中に、下記の \(J_{01}, J_{02}\) がマシンのグラフ制約によってどうしても同時に実現できなかったとします (インデックス1, 2はマッピング済みとします)。
\[ E_0 = J_{01}\sigma_0 \sigma_1 + J_{02} \sigma_0 \sigma_2 \qquad \left( \sigma \in \left\{ -1, +1 \right\} \right) \]その代わりとして \(J_{03}, J_{23}\) は結合可能だった場合、隣接ノードによるチェイン化が有効です。上記の \(J_{02}\sigma_0 \sigma_2\) を置き換えて、
\[ E_0 = J_{01}\sigma_0 \sigma_1 + J_{23} \sigma_2 \sigma_3 \]とします。配置できない \(\sigma_0\) を \(\sigma_3\) で置き換えて、 \(\sigma_2\) と結合させました。つまり、 \(\sigma_0\) と \(\sigma_3\) を同一視して \(J_{23} = J_{02}\) とすれば元の式と一致します。
しかし実際のマシン上では \(\sigma_0\) と \(\sigma_3\) は別の変数です。そこで \(\sigma_0 = \sigma_3\) となるようにペナルティ \(H_p\) を加えます。
\[ H_p = J_{03} \sigma_0 \sigma_3 \qquad \left( J_{03} < 0 \right) \]このペナルティ項は \(\sigma_0\) と \(\sigma_3\) が一致している時にエネルギーが下がり、そうでない場合にエネルギーが上がります。つまり、最もエネルギーの低い最適解については \(\sigma_0 = \sigma_3\) となるような制約が与えられたことになります。
この制約を加味して図示したのが、上右図で繋がった中央の3変数です。この3変数はマシン上では別変数ですが、同じ値になるように強磁性的な相互作用 ( \( J < 0\) ) によって繋がったチェインになっています。
アニーリングマシンの出力は一般的に近似解なので、制約を満たすかは保証されていません。マシンによってはチェイン制約がサポートされている場合もありますが、一般にはユーザがチェックする必要があります。このようにして、解きたいイジング模型のグラフをマシンに実装されたグラフにマッピングしていきます。このマッピングは必ずしも成功するわけではなく、適当に配置していると、時にどうやっても繋ぐことができなくなります。これは、解きたいグラフが本質的にマシンのグラフに配置可能なのか、可能な場合その配置は何かという問題を解く必要が有ることを意味しています。多くの場合この問題に対してはヒューリスティクなアルゴリズムによって対処しているようです。
全結合マッピング #
入力毎にグラフマッピングの問題を対応しなくても、どのようなグラフであれマッピングする方法があります。使用可能なビット変数の数は大幅に少なくなりますが、上で述べたチェインを活用することで、マシンに実装されたグラフを完全グラフ(全結合)に変換することが可能になります。
一般に、二次元規則格子上のノードから完全グラフを作成するには次のような方法が知られています。 \(N\) ノードの完全グラフでは、一つのノードがその他 \(N - 1\) ノードと結合する必要があります。そのため、 \(N\left(N - 1 \right)\) のノードを、 \(N\) 個の長さ \(N - 1\) ノードチェインに分配し、それぞれを1ノードとみなします。
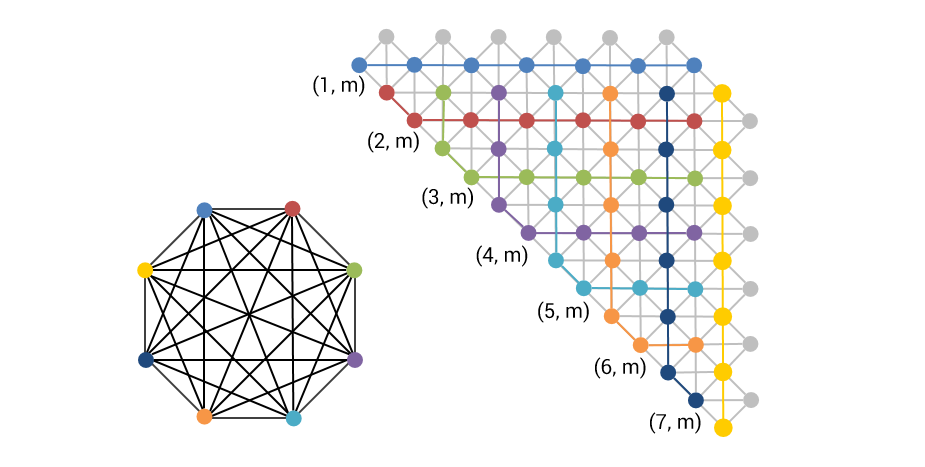
ノードチェイン内のそれぞれのノードは、別のノードチェインとの相互作用を担います。これを二次元規則格子上にうまい具合に配置すると、キンググラフを一例として上図のように構築できます。グラフ上の空白の斜め方向の結合が、それぞれ別のノードチェインとの相互作用を実現します。隣接行列における上三角部分の \(\left(n, m \right)\) 成分をイメージするとわかりやすいと思います。上図の例では、 \(N = 8\) の完全グラフに相当します。
このようなノードチェインを事前に作っておくことで、サイズが許す限りであれば任意のグラフを埋め込むことが可能になります。実際のマシンにおけるグラフにおいても、完全グラフ化をある程度意識した実装になっています。例えば D-Wave のマシンはキメラグラフと呼ばれるグラフ上に量子ビットが配置されています。このグラフは8ノードを1ユニットとして、一つのユニットセルの中はノードが4対4で互いに全結合しています (ただし4つのノード内は結合していません)。つまりサイズ (4, 4) の完全2部グラフに相当します。
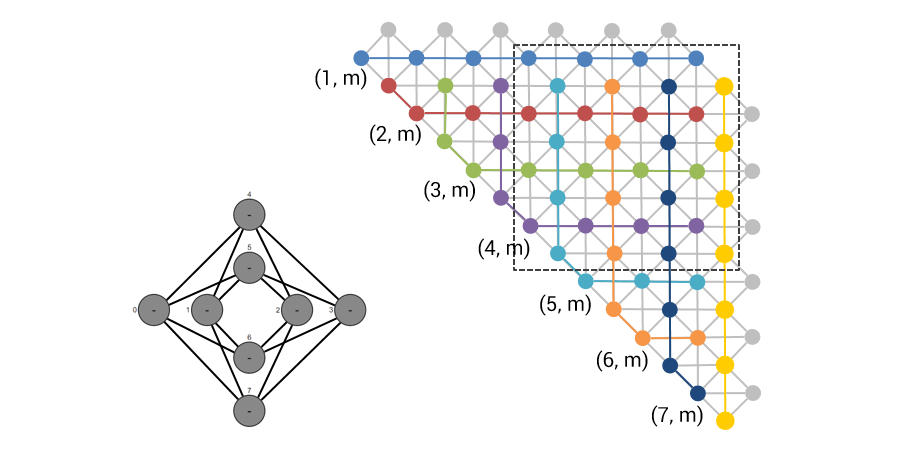
この1ユニットセルは。隣接行列の \(4 \times 4\) 部分に相当します。上図の点線で囲んだ部分の32ノードを8ノードで担うことになります。そのため、このユニットセルがマシン上に \(n \times n\) 配置されているとして、ノード数 \(4 n\) の完全グラフが構築できます。最新の D-Wave 2000Q では、2048 量子ビットを \(16 \times 16\) のユニットセルで構築しています。そのため完全グラフ換算では \(4 \times 16 = 64\) 量子ビットに相当します。
その他の状況としては、日立のマシンは \(20480\) ビットが非全結合で実装されているようです。グラフをキンググラフとした場合、完全グラフ換算でおおよそ 128 ノード以上に相当するものと思われます。