化学プラントにおける生産量最大化

ここでは、Amplify SDK のデモ・チュートリアルで紹介されているブラックボックス最適化サンプルコードを、Amplify-BBOptを使って実装します。

対象とするサンプルコード以下の通りですが、詳しいシミュレーターの構成や、問題設定については以下のデモ・チュートリアルページの解説を参照してください。ここでは、デモ・チュートリアルページで解説されているシミュレーターに基づいて、Amplify-BBOpt を使って同じ最適化をより簡単に実装します。

『ブラックボックス最適化による化学プラントにおける生産量最大化』

ここでは、あるプラント反応装置における生産量の最大化に関する最適化を目的とします。反応装置を構成する反応器内の反応物や生成物の化学反応・輸送現象は、有限差分法による数値シミュレーションによって予測され、その予測結果に基づいて、反応器における物質生成量を最大化するような最適化を行います。

反応器シミュレーションの実装

以下に有限差分法に基づく反応器のシミュレーションクラス Reactor を実装します。本クラスの実装に関しては、基本的に上記デモと同一となります。

Show code cell source

Hide code cell source

import time

import matplotlib.pyplot as plt
import numpy as np

# ある反応性物質 (A->B) の濃度 に関する次の輸送方程式（偏微分方程式）を有限差分法で解くクラス。


class Reactor:
    def __init__(self, nfolds=5, alpha=1.0, dt_prod=1e-3, rr=1e4):
        self.nfolds = (
            nfolds  # シミュレーション領域の空間解像度を決定するパラメータ
        )
        self.alpha = alpha  # 分子拡散係数
        self.dt_prod = dt_prod  # 予め決められた生産時間
        self.rr = rr  # 反応速度に関する係数

    # 2次精度中心差分法により、分布 f の2階微分を求める関数（周期境界条件を仮定）

    def __dfdx2(self, f, dfdx2):
        dfdx2[0] = (f[1] - 2 * f[0] + f[self.nx - 1]) / self.dx / self.dx
        dfdx2[self.nx - 1] = (
            (f[0] - 2 * f[self.nx - 1] + f[self.nx - 2]) / self.dx / self.dx
        )
        dfdx2[1 : self.nx - 1] = (
            np.array([
                f[i + 1] - 2 * f[i] + f[i - 1] for i in range(1, self.nx - 1)
            ])
            / self.dx
            / self.dx
        )
        return dfdx2

    # 場の初期条件を決定

    def __init_field(self, x):
        self.nx = self.nfolds * len(x)  # 空間離散化で用いる格子点数
        self.dx = 1.0 / (self.nx - 1)  # 格子点間隔
        self.concn_A = np.zeros(self.nx)  # Aの濃度分布
        self.concn_B = np.zeros(self.nx)  # Bの濃度分布
        self.x_cord = np.array([
            i / self.nx - 0.5 for i in range(self.nx)
        ])  # 離散点の座標系
        self.concn_A = np.array([
            float(x[i]) for i in range(len(x)) for j in range(self.nfolds)
        ])  # Aの初期場を作成

    # A の初期分布 init_A に応じて、輸送方程式を dt_prod の物理時間だけ時間発展させ、B の総生成量を返す関数

    def integrate(self, init_A, fig=False):
        self.__init_field(init_A)
        start = time.perf_counter()
        omega = np.zeros(self.nx)
        dfdx2 = np.zeros(self.nx)
        dt = (
            0.25 * self.dx * self.dx / self.alpha
        )  # オイラー法での時間ステップ幅
        lts = int(self.dt_prod / dt)
        if fig:  # 反応経過のプロット
            fig = plt.figure(figsize=(6, 4))
            plt.tick_params(labelsize=16)
            plt.xlabel("x", fontsize=16)
            plt.ylabel("Concentration", fontsize=18)
            plt.plot(
                self.x_cord,
                self.concn_A,
                linestyle="-",
                linewidth=1,
                color=[0.6, 0.6, 0.6],
                label="$C_{A,0}$",
            )
        self.iter = 0
        while self.iter * dt < self.dt_prod:
            if fig and any([
                self.iter == i
                for i in [0, int(0.1 * lts), int(0.2 * lts), int(0.4 * lts)]
            ]):  # 反応経過のプロット
                plt.plot(
                    self.x_cord,
                    self.concn_B,
                    linestyle="-",
                    linewidth=2,
                    color="r",
                )
            omega = (
                self.rr
                * np.exp(-self.concn_B)
                * self.concn_A
                * (1.0 - self.concn_A)
            )  # 反応速度
            self.concn_A = (
                self.concn_A
                + (self.alpha * self.__dfdx2(self.concn_A, dfdx2) - omega) * dt
            )  # Aの濃度に関する時間発展
            self.concn_B = (
                self.concn_B
                + (self.alpha * self.__dfdx2(self.concn_B, dfdx2) + omega) * dt
            )  # Bの濃度に関する時間発展
            self.iter += 1
        if fig:  # 反応経過のプロット
            plt.plot(
                self.x_cord,
                self.concn_B,
                linestyle="-",
                linewidth=4,
                color="r",
                label="$C_B$",
            )
            plt.legend(fontsize=16)
        self.cpu_time = (
            time.perf_counter() - start
        )  # シミュレーションに要した時間計測
        return np.sum(self.concn_B) * self.dx  # 濃度の簡易的な空間積分

ブラックボックス関数の実装

ここでは、反応器シミュレータークラス Reactor と、Amplify-BBOpt の @blackbox デコレータを使い、ブラックボックス関数を実装します。

from logging import getLogger
from typing import Annotated

from amplify_bbopt import AMPLIFY_BBOPT_LOGGER_NAME, BinaryVariable, blackbox

logger = getLogger(AMPLIFY_BBOPT_LOGGER_NAME)

input_q = [BinaryVariable() for _ in range(100)]  # バイナリ変数のリスト


# 目的関数 (生成された物質 B の総量の負値を返す)
@blackbox
def my_obj_func(init_a: Annotated[list[int], input_q]) -> float:
    my_reactor = Reactor()
    minus_total = -my_reactor.integrate(init_a, fig=False)
    logger.info(f"{minus_total=:.2e}, {my_reactor.cpu_time=:.1e}s")
    return minus_total

最適化の実行

今回は、サロゲートモデルとして、FMTrainer で考慮可能な FM を採用し、FMQA として、最適化クラスをインスタンス化します。他のサロゲートモデルに関しては、こちらを参照してください。

初期学習データを追加後、最適化サイクルを実行します。

from datetime import timedelta

from amplify import FixstarsClient
from amplify_bbopt import FMTrainer, Optimizer

client = FixstarsClient()
client.parameters.timeout = timedelta(milliseconds=2000)
# client.token = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"  # ローカル環境等で使用する場合は、Amplify AEのアクセストークンを入力してください。

optimizer = Optimizer(my_obj_func, FMTrainer(), client)

num_init_data = 10  # 初期学習データのサンプル数
optimizer.add_random_training_data(num_init_data)

optimizer.optimize(10)

Show code cell output

Hide code cell output

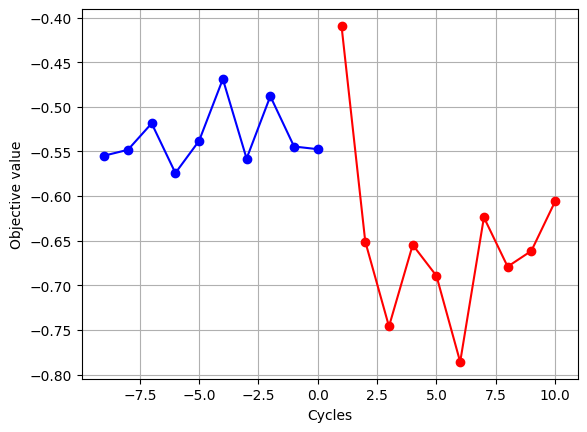
[2025-07-23 14:51:50] [amplify_bbopt] [INFO] Random data sample: 1/10
[2025-07-23 14:51:51] [amplify_bbopt] [INFO] minus_total=-5.55e-01, my_reactor.cpu_time=4.3e-01s
[2025-07-23 14:51:51] [amplify_bbopt] [INFO] Random data sample: 2/10
[2025-07-23 14:51:51] [amplify_bbopt] [INFO] minus_total=-5.48e-01, my_reactor.cpu_time=4.1e-01s
[2025-07-23 14:51:51] [amplify_bbopt] [INFO] Random data sample: 3/10
[2025-07-23 14:51:52] [amplify_bbopt] [INFO] minus_total=-5.19e-01, my_reactor.cpu_time=4.8e-01s
[2025-07-23 14:51:52] [amplify_bbopt] [INFO] Random data sample: 4/10
[2025-07-23 14:51:52] [amplify_bbopt] [INFO] minus_total=-5.74e-01, my_reactor.cpu_time=4.6e-01s
[2025-07-23 14:51:52] [amplify_bbopt] [INFO] Random data sample: 5/10
[2025-07-23 14:51:53] [amplify_bbopt] [INFO] minus_total=-5.38e-01, my_reactor.cpu_time=4.5e-01s
[2025-07-23 14:51:53] [amplify_bbopt] [INFO] Random data sample: 6/10
[2025-07-23 14:51:53] [amplify_bbopt] [INFO] minus_total=-4.69e-01, my_reactor.cpu_time=4.3e-01s
[2025-07-23 14:51:53] [amplify_bbopt] [INFO] Random data sample: 7/10
[2025-07-23 14:51:53] [amplify_bbopt] [INFO] minus_total=-5.58e-01, my_reactor.cpu_time=4.0e-01s
[2025-07-23 14:51:54] [amplify_bbopt] [INFO] Random data sample: 8/10
[2025-07-23 14:51:54] [amplify_bbopt] [INFO] minus_total=-4.88e-01, my_reactor.cpu_time=4.0e-01s
[2025-07-23 14:51:54] [amplify_bbopt] [INFO] Random data sample: 9/10
[2025-07-23 14:51:54] [amplify_bbopt] [INFO] minus_total=-5.44e-01, my_reactor.cpu_time=4.3e-01s
[2025-07-23 14:51:54] [amplify_bbopt] [INFO] Random data sample: 10/10
[2025-07-23 14:51:55] [amplify_bbopt] [INFO] minus_total=-5.47e-01, my_reactor.cpu_time=4.3e-01s
[2025-07-23 14:51:55] [amplify_bbopt] [INFO] === Iteration: 1/10 ===
[2025-07-23 14:52:06] [amplify_bbopt] [INFO] model corrcoefs: <=10%: nan, <=25%: 0.971, <=50%: 0.464, all: -0.366
[2025-07-23 14:52:09] [amplify_bbopt] [INFO] minus_total=-4.09e-01, my_reactor.cpu_time=4.0e-01s
[2025-07-23 14:52:09] [amplify_bbopt] [INFO]    objective: -4.094e-01
[2025-07-23 14:52:09] [amplify_bbopt] [INFO] current best: -5.742e-01
[2025-07-23 14:52:09] [amplify_bbopt] [INFO] === Iteration: 2/10 ===
[2025-07-23 14:52:16] [amplify_bbopt] [INFO] model corrcoefs: <=10%: 1.000, <=25%: 0.994, <=50%: 0.637, all: 0.805
[2025-07-23 14:52:19] [amplify_bbopt] [INFO] minus_total=-6.51e-01, my_reactor.cpu_time=4.2e-01s
[2025-07-23 14:52:19] [amplify_bbopt] [INFO]    objective: -6.509e-01
[2025-07-23 14:52:19] [amplify_bbopt] [INFO] current best: -6.509e-01
[2025-07-23 14:52:19] [amplify_bbopt] [INFO] === Iteration: 3/10 ===
[2025-07-23 14:52:25] [amplify_bbopt] [INFO] model corrcoefs: <=10%: 1.000, <=25%: 1.000, <=50%: 1.000, all: 0.867
[2025-07-23 14:52:28] [amplify_bbopt] [INFO] minus_total=-7.46e-01, my_reactor.cpu_time=4.2e-01s
[2025-07-23 14:52:28] [amplify_bbopt] [INFO]    objective: -7.461e-01
[2025-07-23 14:52:28] [amplify_bbopt] [INFO] current best: -7.461e-01
[2025-07-23 14:52:28] [amplify_bbopt] [INFO] === Iteration: 4/10 ===
[2025-07-23 14:52:35] [amplify_bbopt] [INFO] model corrcoefs: <=10%: 1.000, <=25%: 1.000, <=50%: 0.925, all: 0.967
[2025-07-23 14:52:38] [amplify_bbopt] [INFO] minus_total=-6.55e-01, my_reactor.cpu_time=4.1e-01s
[2025-07-23 14:52:38] [amplify_bbopt] [INFO]    objective: -6.547e-01
[2025-07-23 14:52:38] [amplify_bbopt] [INFO] current best: -7.461e-01
[2025-07-23 14:52:38] [amplify_bbopt] [INFO] === Iteration: 5/10 ===
[2025-07-23 14:52:47] [amplify_bbopt] [INFO] model corrcoefs: <=10%: 1.000, <=25%: 0.999, <=50%: 1.000, all: 0.986
[2025-07-23 14:52:50] [amplify_bbopt] [INFO] minus_total=-6.89e-01, my_reactor.cpu_time=4.4e-01s
[2025-07-23 14:52:50] [amplify_bbopt] [INFO]    objective: -6.894e-01
[2025-07-23 14:52:50] [amplify_bbopt] [INFO] current best: -7.461e-01
[2025-07-23 14:52:50] [amplify_bbopt] [INFO] === Iteration: 6/10 ===
[2025-07-23 14:52:59] [amplify_bbopt] [INFO] model corrcoefs: <=10%: 1.000, <=25%: 0.910, <=50%: 0.986, all: 0.920
[2025-07-23 14:53:02] [amplify_bbopt] [INFO] minus_total=-7.86e-01, my_reactor.cpu_time=4.3e-01s
[2025-07-23 14:53:02] [amplify_bbopt] [INFO]    objective: -7.859e-01
[2025-07-23 14:53:02] [amplify_bbopt] [INFO] current best: -7.859e-01
[2025-07-23 14:53:02] [amplify_bbopt] [INFO] === Iteration: 7/10 ===
[2025-07-23 14:53:09] [amplify_bbopt] [INFO] model corrcoefs: <=10%: 1.000, <=25%: 1.000, <=50%: 0.874, all: 0.808
[2025-07-23 14:53:14] [amplify_bbopt] [INFO] minus_total=-6.24e-01, my_reactor.cpu_time=4.0e-01s
[2025-07-23 14:53:14] [amplify_bbopt] [INFO]    objective: -6.239e-01
[2025-07-23 14:53:14] [amplify_bbopt] [INFO] current best: -7.859e-01
[2025-07-23 14:53:14] [amplify_bbopt] [INFO] === Iteration: 8/10 ===
[2025-07-23 14:53:22] [amplify_bbopt] [INFO] model corrcoefs: <=10%: 1.000, <=25%: 0.638, <=50%: 0.856, all: 0.840
[2025-07-23 14:53:24] [amplify_bbopt] [INFO] minus_total=-6.79e-01, my_reactor.cpu_time=4.0e-01s
[2025-07-23 14:53:24] [amplify_bbopt] [INFO]    objective: -6.791e-01
[2025-07-23 14:53:24] [amplify_bbopt] [INFO] current best: -7.859e-01
[2025-07-23 14:53:24] [amplify_bbopt] [INFO] === Iteration: 9/10 ===
[2025-07-23 14:53:32] [amplify_bbopt] [INFO] model corrcoefs: <=10%: 1.000, <=25%: 0.994, <=50%: 0.660, all: 0.884
[2025-07-23 14:53:35] [amplify_bbopt] [INFO] minus_total=-6.61e-01, my_reactor.cpu_time=4.2e-01s
[2025-07-23 14:53:35] [amplify_bbopt] [INFO]    objective: -6.615e-01
[2025-07-23 14:53:35] [amplify_bbopt] [INFO] current best: -7.859e-01
[2025-07-23 14:53:35] [amplify_bbopt] [INFO] === Iteration: 10/10 ===
[2025-07-23 14:53:42] [amplify_bbopt] [INFO] model corrcoefs: <=10%: 1.000, <=25%: -0.028, <=50%: 0.114, all: 0.419
[2025-07-23 14:53:46] [amplify_bbopt] [INFO] minus_total=-6.06e-01, my_reactor.cpu_time=4.2e-01s
[2025-07-23 14:53:46] [amplify_bbopt] [INFO]    objective: -6.060e-01
[2025-07-23 14:53:46] [amplify_bbopt] [INFO] current best: -7.859e-01

最適化履歴のプロット

多くのイジングマシンに採用されている、ヒューリスティクスというアルゴリズムの原理上、得られる解に完全な再現性はありませんが、本サンプルコードを実行した際に得られる、典型的な標準出力及び画像出力を以下に紹介します。

当該のデモチュートリアルと同様の最適化結果を得ることができました。

# 初期学習データの履歴
objective_init = optimizer.training_data.y[:num_init_data]

# アニーリングから直接得られた最良解の履歴
objective_anneal = [
    float(h.annealing_best_solution.objective) for h in optimizer.history
]

plt.plot(range(-num_init_data + 1, 1), objective_init, "-ob")
plt.plot(range(1, len(objective_anneal) + 1), objective_anneal, "-or")
plt.xlabel("Cycles")
plt.ylabel("Objective value")
plt.grid(True)

Hint

今回のブラックボックス関数では、関数値の値域が \(-1 \le y\le0\) であることが明らかです。最適化性能向上を目的として、「transformation.md」の変換を実施する場合は、以下のように指数変換前に0がターゲットの目的関数値となる様にオフセットするとよいでしょう。

\[ y^* = y + 1 \]

\[ \hat{y}=-\exp\left(\frac{-y^*}{c_m}\right) \]