Quadratic Assignment Problem

Quadratic assignment problem (QAP) is the following problem.

Quadratic assignment problem

Let \(N\) be a positive integer. Consider \(N\) factories to be built on \(N\) candidate sites. Each factory can be built on any of the candidate sites. Every two factories have trucks traveling to and from them, and their transportation volumes are known in advance. How can we minimize the sum of the amount transported x the distance traveled?

An application could be to determine the seating chart for a meeting so that people close to each other have seats closely.

Formulation

Let \(N\) potential factory locations be denoted by land \(0\), land \(1\), … , and \(N\) factories are denoted as factories \(0\), factories \(1\), …, factories \(N-1\). Also let \(D_{i, j}\) denote the distance between land \(i\) and land \(j\), and \(F_{k, l}\) denote the transport volume between factory \(k\) and factory \(l\).

Variables

With \(N \times N\) binary variables \(q\), let \(q_{i, k}\) represent whether factory \(k\) is to be built on land \(i\).

For example, factory \(3\) will be built on land \(0\) if \(q\) has the following value.

Binary variable table

	factory 0	factory 1	factory 2	factory 3	factory 4
land 0	0	0	0	1	0
land 1	0	1	0	0	0
land 2	0	0	0	0	1
land 3	1	0	0	0	0
land 4	0	0	1	0	0

Constraints

Each row and column of the binary variable table must have exactly one variable that is 1, so we place a one-hot constraint on each row and column. Conversely, if these are satisfied, then there is only one way to determine which factory to build on which land.

Objective function

The objective function is the sum of transport volume x distance between factories. This can be expressed in the equation using \(q\) as follows.

\[ \sum_{q_{i, k} = 1, q_{j, l} = 1} D_{i, j} \ F_{k, l} = \sum_{i, j, k, l} q_{i, k} \ q_{j, l} \ D_{i, j} \ F_{k, l} \]

Formulation

The above formulation, with \(N\times N\) binary variables \(q\), can be written as follows.

\[\begin{split} \begin{align} \text{minimize} \quad &\sum_{i, j, k, l} q_{i, k} \ q_{j, l} \ D_{i, j} \ F_{k, l} \\ \text{subject to} \quad &\sum_k q_{i, k} = 1 \quad \text{for} \quad i \in \{0, 1, \ldots, N - 1\}, \\ &\sum_i q_{i, k} = 1 \quad \text{for} \quad k \in \{0, 1, \ldots, N - 1\}, \\ &q_{i, k} \in \{0, 1\} \quad \text{for} \quad i, k \in \{0, 1, \ldots, N - 1\}. \end{align} \end{split}\]

Problem setting

Before formulating with the Amplify SDK, we will create a problem. For simplicity, let the number of factories \(N=10\).

import numpy as np

N = 10

Next, we create a distance matrix \(D\) representing the distances between lands. The lands are randomly generated on the Euclidean plane. The distance matrix distance is created as a two-dimensional numpy.ndarray.

rng = np.random.default_rng()

x = rng.integers(0, 100, size=(N,))
y = rng.integers(0, 100, size=(N,))

distance = (
    (x[:, np.newaxis] - x[np.newaxis, :]) ** 2
    + (y[:, np.newaxis] - y[np.newaxis, :]) ** 2
) ** 0.5

print(distance)

[[ 0.         51.2445119  69.3181073  31.76476035 10.19803903  4.12310563
  70.60453243 63.07138812 54.34151268 70.17834424]
 [51.2445119   0.         79.07591289 36.40054945 56.79788728 53.48831648
  71.25307011 18.43908891 27.29468813 68.0661443 ]
 [69.3181073  79.07591289  0.         91.41115906 61.58733636 66.24198065
  13.41640786 72.44998275 54.62600113 17.49285568]
 [31.76476035 36.40054945 91.41115906  0.         41.62931659 35.77708764
  88.54377448 54.12023651 55.1724569  86.72946443]
 [10.19803903 56.79788728 61.58733636 41.62931659  0.          6.08276253
  64.35060217 66.28725368 55.03635162 64.44377394]
 [ 4.12310563 53.48831648 66.24198065 35.77708764  6.08276253  0.
  68.11754546 64.38167441 54.58937626 67.89698079]
 [70.60453243 71.25307011 13.41640786 88.54377448 64.35060217 68.11754546
   0.         62.29767251 45.12205669  4.24264069]
 [63.07138812 18.43908891 72.44998275 54.12023651 66.28725368 64.38167441
  62.29767251  0.         18.02775638 58.52349955]
 [54.34151268 27.29468813 54.62600113 55.1724569  55.03635162 54.58937626
  45.12205669 18.02775638  0.         41.59326869]
 [70.17834424 68.0661443  17.49285568 86.72946443 64.44377394 67.89698079
   4.24264069 58.52349955 41.59326869  0.        ]]

Also, we create a matrix \(F\) representing the amount of transport between factories, a random symmetric matrix of dimension 2, named flow.

flow = np.zeros((N, N), dtype=int)
for i in range(N):
    for j in range(i + 1, N):
        flow[i, j] = flow[j, i] = rng.integers(0, 100)

print(flow)

[[ 0 39 11 36 53  6 73 72 34 58]
 [39  0 47 40 45 77 25 59  6 66]
 [11 47  0 22 39 77 38 70 33 20]
 [36 40 22  0  1 34 66 96  6 63]
 [53 45 39  1  0 65 84 85 35  2]
 [ 6 77 77 34 65  0 12 45 13 36]
 [73 25 38 66 84 12  0 59 43 61]
 [72 59 70 96 85 45 59  0 56 17]
 [34  6 33  6 35 13 43 56  0 98]
 [58 66 20 63  2 36 61 17 98  0]]

Formulation with the Amplify SDK

In the formulation, we can use the Matrix class for efficient formulation, since a quadratic term consisting of any two binary variables can appear in the objective function.

Creating variables

To formulate using the Matrix class, VariableGenerator’s matrix() method to issue variables.

from amplify import VariableGenerator

gen = VariableGenerator()
matrix = gen.matrix("Binary", N, N)  # coefficient matrix
q = matrix.variable_array  # variables

q

\[\begin{split}\displaystyle \begin{aligned}&\left[\begin{matrix}q_{0,0}& q_{0,1}& q_{0,2}& q_{0,3}& q_{0,4}& q_{0,5}& q_{0,6}& q_{0,7}& q_{0,8}& q_{0,9}\\q_{1,0}& q_{1,1}& q_{1,2}& q_{1,3}& q_{1,4}& q_{1,5}& q_{1,6}& q_{1,7}& q_{1,8}& q_{1,9}\\q_{2,0}& q_{2,1}& q_{2,2}& q_{2,3}& q_{2,4}& q_{2,5}& q_{2,6}& q_{2,7}& q_{2,8}& q_{2,9}\\q_{3,0}& q_{3,1}& q_{3,2}& q_{3,3}& q_{3,4}& q_{3,5}& q_{3,6}& q_{3,7}& q_{3,8}& q_{3,9}\\q_{4,0}& q_{4,1}& q_{4,2}& q_{4,3}& q_{4,4}& q_{4,5}& q_{4,6}& q_{4,7}& q_{4,8}& q_{4,9}\\q_{5,0}& q_{5,1}& q_{5,2}& q_{5,3}& q_{5,4}& q_{5,5}& q_{5,6}& q_{5,7}& q_{5,8}& q_{5,9}\\q_{6,0}& q_{6,1}& q_{6,2}& q_{6,3}& q_{6,4}& q_{6,5}& q_{6,6}& q_{6,7}& q_{6,8}& q_{6,9}\\q_{7,0}& q_{7,1}& q_{7,2}& q_{7,3}& q_{7,4}& q_{7,5}& q_{7,6}& q_{7,7}& q_{7,8}& q_{7,9}\\q_{8,0}& q_{8,1}& q_{8,2}& q_{8,3}& q_{8,4}& q_{8,5}& q_{8,6}& q_{8,7}& q_{8,8}& q_{8,9}\\q_{9,0}& q_{9,1}& q_{9,2}& q_{9,3}& q_{9,4}& q_{9,5}& q_{9,6}& q_{9,7}& q_{9,8}& q_{9,9}\end{matrix}\right]\end{aligned}\end{split}\]

Creating the objective function

The matrix created above is an instance of the class Matrix, which has the following three properties.

• quadratic

• linear

• constant

quadratic is numpy.ndarray representing the coefficients of the second order terms, and its shape is (N, N, N, N) this time. quadratic[i, k, j, l] corresponds to the coefficients of q[i, k] * q[j, l]. That is, quadratic must be set to a 4-dimensional NumPy array such that quadratic[i, k, j, l] = distance[i, j] * flow[k, l]

linear and constant represent the coefficient and constant terms of the linear term, respectively, but since the objective function used in this problem contains only second order terms, we will not set them.

np.einsum("ij,kl->ikjl", distance, flow, out=matrix.quadratic)

Creating constraints

Impose a one-hot constraint on each row and column of the variable array q created in [](#Creating variables).

from amplify import one_hot

constraints = one_hot(q, axis=1) + one_hot(q, axis=0)

Creating a combinatorial optimization model

Let’s combine the objective function and constraints to create a model.

penalty_weight = np.max(distance) * np.max(flow) * (N - 1)
model = matrix + penalty_weight * constraints

The penalty_weight is applied to the constraints to give weight to the constraints. In Amplify AE, the solver used in this example, if you do not specify appropriate weights for the constraints, the solver will search in the direction of making the objective function smaller rather than trying to satisfy the constraints, and you will not be able to find a feasible solution. See Constraints and Penalty Functions for details.

Creating a solver client

Now, we will create a solver client to perform combinatorial optimization using Amplify AE. The solver client class corresponding to Amplify AE is AmplifyAEClient class.

from amplify import AmplifyAEClient

client = AmplifyAEClient()

We also need to set the API token required to run Amplify AE.

Tip

After user registration, you can obtain a free API token that can be used for evaluation and validation purposes.

client.token = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"

We will set the solver’s timeout.

import datetime

client.parameters.time_limit_ms = datetime.timedelta(seconds=1)

Executing the solver

Finally, we will execute the solver using the created combinatorial optimization model and the solver client to find the solution to the quadratic programming problem.

from amplify import solve

result = solve(model, client)

The objective function value based on the best solution is shown below.

result.best.objective

177482.42495235227

The values of the variables in the optimal solution can be obtained in the form of a NumPy multidimensional array as follows.

q_values = q.evaluate(result.best.values)

print(q_values)

[[0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
 [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]]

Checking the results

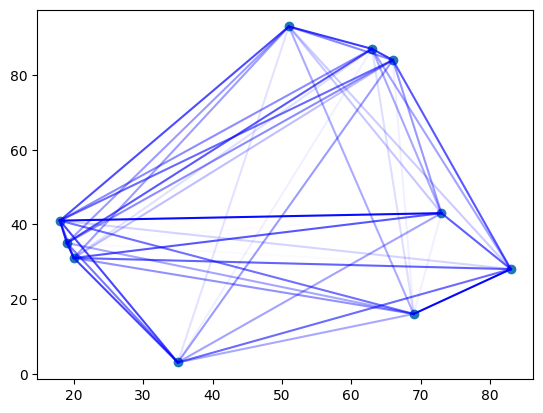
We will visualize the results using matplotlib.

import itertools

import matplotlib.pyplot as plt

plt.scatter(x, y)
factory_indices = (q_values @ np.arange(N)).astype(int)

for i, j in itertools.combinations(range(N), 2):
    plt.plot(
        [x[i], x[j]],
        [y[i], y[j]],
        c="b",
        alpha=flow[factory_indices[i], factory_indices[j]] / 100,
    )