巡回セールスマン問題¶
Amplify の使用例として、巡回セールスマン問題を Amplify を用いて解く方法を解説します。 巡回セールスマン問題とは、いくつかの都市の集合が与えられたとき、ある都市から出発してすべての都市を 1 回ずつ訪れたあと最初の都市に戻ってくる巡回路のうち、最も長さが短いものを求める組合せ最適化問題です。
巡回セールスマン問題の定式化¶
以下では、都市の数を NUM_CITIES と表記します。
変数¶
まず、NUM_CITIES 個の都市のうちどの都市を訪れるかを表すために、 NUM_CITIES 個のバイナリ (0-1) 変数を用いることにします。都市 i を訪れる場合、i 番目のバイナリ変数を 1 、それ以外の変数を 0 とすることで表現します。
たとえば都市数が 5 であり 5 つのバイナリ変数の値が [0, 0, 0, 1, 0] の場合、インデックス 3 の変数のみが 1 となっているので都市 3 を訪れることの表現となっています。このように、n 個の選択肢の中からどれを選ぶかを n 個のバイナリ変数のうち 1 つを 1 にすることで表す方法を one-hot エンコーディングといい、機械学習などでもよく使われます。
都市 0 |
都市 1 |
都市 2 |
都市 3 |
都市 4 |
|---|---|---|---|---|
0 |
0 |
0 |
1 |
0 |
巡回路では都市を 1 回ずつ訪れて最後に最初の都市に戻ってくるので、最初と最後も含めて NUM_CITIES + 1 回都市を訪れることになります。したがって、 (NUM_CITIES + 1) * NUM_CITIES 個のバイナリ変数を用意します。たとえば以下の例は、都市 3 → 都市 1 → 都市 4 → 都市 0 → 都市 2 → 都市 3 の順に 5 つの都市を訪れる巡回路を表現します。
都市 0 |
都市 1 |
都市 2 |
都市 3 |
都市 4 |
|---|---|---|---|---|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
制約条件¶
上の「バイナリ変数表」において、(NUM_CITIES + 1) * NUM_CITIES 個のバイナリ変数が好き勝手に 0 または 1 の値をとっても巡回路の表現になるとは限りません。たとえば、すべてのバイナリ変数の値が 1 であるとき、何の巡回路も表しません。したがって、バイナリ変数に制約を課す必要があります。必要な制約は以下の 3 種類です。
バイナリ変数表の最初の行と最後の行は、同じ値をとる。
バイナリ変数表の各行のうち、値が 1 となっている箇所はちょうど 1 つだけである。
バイナリ変数表の各列において、値が 1 となっている箇所は最後の行を除きちょうど 1 つだけである。
逆に、以上の 3 つの制約をみたしているバイナリ変数表があるとき、それはある巡回路の表現となっています。
目的関数¶
巡回セールスマン問題の目的は、巡回路のうち最も経路長が短いものを探すことです。したがって、目的関数は巡回路の経路長となります。
都市 i と都市 j の距離が d[i, j] であるとします。現在のゴールは、バイナリ変数表の値から巡回路の経路長を求めることです。
バイナリ変数表の値が分かっている場合、巡回路の経路長は以下の疑似コードのようにして求められます。ただし、k 行 i 列のバイナリ変数が q[k, i] と書けるとします。
route_length = 0
for k in range(NUM_CITIES):
for i in range(NUM_CITIES):
for j in range(NUM_CITIES):
route_length += (d[i, j] if q[k, i] == 1 and q[k+1, j] == 1 else 0)
しかし Amplify で定式化を行う場合、それぞれの q[k, i] はバイナリ変数であることが分かっているのみでまだ何の値を取るかは分からないので、if q[k, i] == 1 and q[k+1, j] == 1 という条件式の判定を行うことはできません。バイナリ変数や数値の足し算および掛け算で目的関数を表す必要があります。
ここで、2 つのバイナリ変数の積 q[k, i] * q[k+1, j] は q[k, i] == 1 and q[k+1, j] == 1 が True のとき 1 となり、False のときは 0 となることを思い出します。すると、目的関数は
route_length = 0
for k in range(NUM_CITIES):
for i in range(NUM_CITIES):
for j in range(NUM_CITIES):
route_length += d[i, j] * q[k, i] * q[k+1, j]
と書くことができることが分かります。
定式化¶
以上の議論を数式で書き下すと、巡回セールスマン問題の定式化は (NUM_CITIES + 1) * NUM_CITIES 個のバイナリ変数を用いて
となります。ただし表記の都合上、都市数 NUM_CITIES を \(N\) と表記しています。
問題の作成¶
まず、問題を作成します。都市数を NUM_CITIES として、それぞれの都市の x 座標と y 座標を 0~100 の整数の中からランダムに選びます。以下では、都市の名前を都市 0, 都市 1, ..., 都市 NUM_CITIES - 1 と呼ぶことにします。
本サンプルコードでは、簡単のため都市数を 5 とします。
import numpy as np
NUM_CITIES = 5
rng = np.random.default_rng()
x = rng.integers(0, 100, NUM_CITIES)
y = rng.integers(0, 100, NUM_CITIES)
次に、都市間の距離を表す距離行列を作成します。距離はユークリッド距離を用います。出力は n * n の NumPy 配列で、i 行 j 列の要素は都市 i と都市 j 間の距離、すなわち (x[i] - x[j]) ** 2 + (y[i] - y[j] ** 2) ** 0.5 を表します。
distance = (
(x[:, np.newaxis] - x[np.newaxis, :]) ** 2
+ (y[:, np.newaxis] - y[np.newaxis, :]) ** 2
) ** 0.5
print(distance)
[[ 0. 35.171 16.279 36.069 8.602]
[35.171 0. 37.656 19.235 41.195]
[16.279 37.656 0. 29.732 11.705]
[36.069 19.235 29.732 0. 38.275]
[ 8.602 41.195 11.705 38.275 0. ]]
Amplify SDK による定式化¶
Amplify SDK を用いた定式化を行います。
変数の生成 ¶
まず、決定変数を作成します。(NUM_CITIES + 1) * NUM_CITIES 個のバイナリ変数が必要です。Amplify SDK では、VariableGenerator を使用することにより 2 次元配列の形で変数を生成することができます。
from amplify import VariableGenerator
gen = VariableGenerator()
q = gen.array("Binary", (NUM_CITIES + 1, NUM_CITIES))
バイナリ変数 q を表示してみると、以下のようになります。
q
制約条件の作成 ¶
次に、制約条件を作成します。前述の通り、作成するべき制約条件は以下の 3 種類です。
バイナリ変数表の最初の行と最後の行は、同じ値をとる。
バイナリ変数表の各行のうち、値が 1 となっている箇所はちょうど 1 つだけである。
バイナリ変数表の各列において、値が 1 となっている箇所は最後の行を除きちょうど 1 つだけである。
1 つ目の制約条件¶
1 つ目の制約条件「バイナリ変数表の最初の行と最後の行は、同じ値をとる。」を作成します。最後の行を最初の行と同じ値に固定したいので、q の最後の行に最初の行を代入します。q の最初の行は q[0]、q の最後の行は q[-1] と書くことができます。
q[-1] = q[0]
q
これで 1 つ目の制約条件を表現することができました。
注意
このように代入により変数を固定する操作を行う場合、目的関数や他の制約条件を構築する前に行ってください。
これ以降の制約条件の作成においては、バイナリ変数配列 q の最後の行のことは考える必要がないため、q の上から NUM_CITIES 行を切り出した配列を作成しておきます。
q_upper = q[:-1]
q_upper
2 つ目の制約条件¶
2 つ目の制約条件「バイナリ変数表の各行のうち、値が 1 となっている箇所はちょうど 1 つだけである。」を作成します。いくつかのバイナリ変数のうちちょうど 1 つだけが 1 であるという制約条件を課したい場合、one_hot() 関数を使います。変数配列の各行に対して one-hot 制約を課したい場合、one_hot() 関数の axis キーワード引数に 1 を与えます。
from amplify import one_hot
constraints2 = one_hot(q_upper, axis=1)
constraints2
NUM_CITIES (= 5) 個の制約条件が一気に生成されました。
3 つ目の制約条件¶
3 つ目の制約条件「バイナリ変数表の各列において、値が 1 となっている箇所は最後の行を除きちょうど 1 つだけである。」を作成します。2 つ目の制約条件と同様に、one_hot() 関数を使います。変数配列の各列に対して one-hot 制約を課したい場合、one_hot() 関数の axis キーワード引数に 0 を与えます。
constraints3 = one_hot(q_upper, axis=0)
constraints3
目的関数の作成 ¶
次に、目的関数を作成します。前述の通り、目的関数は巡回路の経路長であり、以下のように書くことができます。
route_length = 0
for k in range(NUM_CITIES):
for i in range(NUM_CITIES):
for j in range(NUM_CITIES):
route_length += distance[i, j] * q[k, i] * q[k + 1, j]
print(route_length)
35.1710107901379 q_{0,0} q_{1,1} + 16.2788205960997 q_{0,0} q_{1,2} + 36.0693775937429 q_{0,0} q_{1,3} + 8.60232526704263 q_{0,0} q_{1,4} + 35.1710107901379 q_{0,0} q_{4,1} + 16.2788205960997 q_{0,0} q_{4,2} + 36.0693775937429 q_{0,0} q_{4,3} + 8.60232526704263 q_{0,0} q_{4,4} + 35.1710107901379 q_{0,1} q_{1,0} + 37.6563407675255 q_{0,1} q_{1,2} + 19.2353840616713 q_{0,1} q_{1,3} + 41.194659848092 q_{0,1} q_{1,4} + 35.1710107901379 q_{0,1} q_{4,0} + 37.6563407675255 q_{0,1} q_{4,2} + 19.2353840616713 q_{0,1} q_{4,3} + 41.194659848092 q_{0,1} q_{4,4} + 16.2788205960997 q_{0,2} q_{1,0} + 37.6563407675255 q_{0,2} q_{1,1} + 29.732137494637 q_{0,2} q_{1,3} + 11.7046999107196 q_{0,2} q_{1,4} + 16.2788205960997 q_{0,2} q_{4,0} + 37.6563407675255 q_{0,2} q_{4,1} + 29.732137494637 q_{0,2} q_{4,3} + 11.7046999107196 q_{0,2} q_{4,4} + 36.0693775937429 q_{0,3} q_{1,0} + 19.2353840616713 q_{0,3} q_{1,1} + 29.732137494637 q_{0,3} q_{1,2} + 38.2753184180093 q_{0,3} q_{1,4} + 36.0693775937429 q_{0,3} q_{4,0} + 19.2353840616713 q_{0,3} q_{4,1} + 29.732137494637 q_{0,3} q_{4,2} + 38.2753184180093 q_{0,3} q_{4,4} + 8.60232526704263 q_{0,4} q_{1,0} + 41.194659848092 q_{0,4} q_{1,1} + 11.7046999107196 q_{0,4} q_{1,2} + 38.2753184180093 q_{0,4} q_{1,3} + 8.60232526704263 q_{0,4} q_{4,0} + 41.194659848092 q_{0,4} q_{4,1} + 11.7046999107196 q_{0,4} q_{4,2} + 38.2753184180093 q_{0,4} q_{4,3} + 35.1710107901379 q_{1,0} q_{2,1} + 16.2788205960997 q_{1,0} q_{2,2} + 36.0693775937429 q_{1,0} q_{2,3} + 8.60232526704263 q_{1,0} q_{2,4} + 35.1710107901379 q_{1,1} q_{2,0} + 37.6563407675255 q_{1,1} q_{2,2} + 19.2353840616713 q_{1,1} q_{2,3} + 41.194659848092 q_{1,1} q_{2,4} + 16.2788205960997 q_{1,2} q_{2,0} + 37.6563407675255 q_{1,2} q_{2,1} + 29.732137494637 q_{1,2} q_{2,3} + 11.7046999107196 q_{1,2} q_{2,4} + 36.0693775937429 q_{1,3} q_{2,0} + 19.2353840616713 q_{1,3} q_{2,1} + 29.732137494637 q_{1,3} q_{2,2} + 38.2753184180093 q_{1,3} q_{2,4} + 8.60232526704263 q_{1,4} q_{2,0} + 41.194659848092 q_{1,4} q_{2,1} + 11.7046999107196 q_{1,4} q_{2,2} + 38.2753184180093 q_{1,4} q_{2,3} + 35.1710107901379 q_{2,0} q_{3,1} + 16.2788205960997 q_{2,0} q_{3,2} + 36.0693775937429 q_{2,0} q_{3,3} + 8.60232526704263 q_{2,0} q_{3,4} + 35.1710107901379 q_{2,1} q_{3,0} + 37.6563407675255 q_{2,1} q_{3,2} + 19.2353840616713 q_{2,1} q_{3,3} + 41.194659848092 q_{2,1} q_{3,4} + 16.2788205960997 q_{2,2} q_{3,0} + 37.6563407675255 q_{2,2} q_{3,1} + 29.732137494637 q_{2,2} q_{3,3} + 11.7046999107196 q_{2,2} q_{3,4} + 36.0693775937429 q_{2,3} q_{3,0} + 19.2353840616713 q_{2,3} q_{3,1} + 29.732137494637 q_{2,3} q_{3,2} + 38.2753184180093 q_{2,3} q_{3,4} + 8.60232526704263 q_{2,4} q_{3,0} + 41.194659848092 q_{2,4} q_{3,1} + 11.7046999107196 q_{2,4} q_{3,2} + 38.2753184180093 q_{2,4} q_{3,3} + 35.1710107901379 q_{3,0} q_{4,1} + 16.2788205960997 q_{3,0} q_{4,2} + 36.0693775937429 q_{3,0} q_{4,3} + 8.60232526704263 q_{3,0} q_{4,4} + 35.1710107901379 q_{3,1} q_{4,0} + 37.6563407675255 q_{3,1} q_{4,2} + 19.2353840616713 q_{3,1} q_{4,3} + 41.194659848092 q_{3,1} q_{4,4} + 16.2788205960997 q_{3,2} q_{4,0} + 37.6563407675255 q_{3,2} q_{4,1} + 29.732137494637 q_{3,2} q_{4,3} + 11.7046999107196 q_{3,2} q_{4,4} + 36.0693775937429 q_{3,3} q_{4,0} + 19.2353840616713 q_{3,3} q_{4,1} + 29.732137494637 q_{3,3} q_{4,2} + 38.2753184180093 q_{3,3} q_{4,4} + 8.60232526704263 q_{3,4} q_{4,0} + 41.194659848092 q_{3,4} q_{4,1} + 11.7046999107196 q_{3,4} q_{4,2} + 38.2753184180093 q_{3,4} q_{4,3}
あるいは、以下のように書いても同じ効果があります。こちらの方が Amplify SDK の機能をフルに活用しているため高速で、NumPy ライブラリに馴染みがある方には特におすすめです。詳細は定式化の高速化を参照してください。
from amplify import Poly, einsum
q1 = q[:-1]
q2 = q[1:]
route_length: Poly = einsum("ij,ki,kj->", distance, q1, q2) # type: ignore
print(route_length)
35.1710107901379 q_{0,0} q_{1,1} + 16.2788205960997 q_{0,0} q_{1,2} + 36.0693775937429 q_{0,0} q_{1,3} + 8.60232526704263 q_{0,0} q_{1,4} + 35.1710107901379 q_{0,0} q_{4,1} + 16.2788205960997 q_{0,0} q_{4,2} + 36.0693775937429 q_{0,0} q_{4,3} + 8.60232526704263 q_{0,0} q_{4,4} + 35.1710107901379 q_{0,1} q_{1,0} + 37.6563407675255 q_{0,1} q_{1,2} + 19.2353840616713 q_{0,1} q_{1,3} + 41.194659848092 q_{0,1} q_{1,4} + 35.1710107901379 q_{0,1} q_{4,0} + 37.6563407675255 q_{0,1} q_{4,2} + 19.2353840616713 q_{0,1} q_{4,3} + 41.194659848092 q_{0,1} q_{4,4} + 16.2788205960997 q_{0,2} q_{1,0} + 37.6563407675255 q_{0,2} q_{1,1} + 29.732137494637 q_{0,2} q_{1,3} + 11.7046999107196 q_{0,2} q_{1,4} + 16.2788205960997 q_{0,2} q_{4,0} + 37.6563407675255 q_{0,2} q_{4,1} + 29.732137494637 q_{0,2} q_{4,3} + 11.7046999107196 q_{0,2} q_{4,4} + 36.0693775937429 q_{0,3} q_{1,0} + 19.2353840616713 q_{0,3} q_{1,1} + 29.732137494637 q_{0,3} q_{1,2} + 38.2753184180093 q_{0,3} q_{1,4} + 36.0693775937429 q_{0,3} q_{4,0} + 19.2353840616713 q_{0,3} q_{4,1} + 29.732137494637 q_{0,3} q_{4,2} + 38.2753184180093 q_{0,3} q_{4,4} + 8.60232526704263 q_{0,4} q_{1,0} + 41.194659848092 q_{0,4} q_{1,1} + 11.7046999107196 q_{0,4} q_{1,2} + 38.2753184180093 q_{0,4} q_{1,3} + 8.60232526704263 q_{0,4} q_{4,0} + 41.194659848092 q_{0,4} q_{4,1} + 11.7046999107196 q_{0,4} q_{4,2} + 38.2753184180093 q_{0,4} q_{4,3} + 35.1710107901379 q_{1,0} q_{2,1} + 16.2788205960997 q_{1,0} q_{2,2} + 36.0693775937429 q_{1,0} q_{2,3} + 8.60232526704263 q_{1,0} q_{2,4} + 35.1710107901379 q_{1,1} q_{2,0} + 37.6563407675255 q_{1,1} q_{2,2} + 19.2353840616713 q_{1,1} q_{2,3} + 41.194659848092 q_{1,1} q_{2,4} + 16.2788205960997 q_{1,2} q_{2,0} + 37.6563407675255 q_{1,2} q_{2,1} + 29.732137494637 q_{1,2} q_{2,3} + 11.7046999107196 q_{1,2} q_{2,4} + 36.0693775937429 q_{1,3} q_{2,0} + 19.2353840616713 q_{1,3} q_{2,1} + 29.732137494637 q_{1,3} q_{2,2} + 38.2753184180093 q_{1,3} q_{2,4} + 8.60232526704263 q_{1,4} q_{2,0} + 41.194659848092 q_{1,4} q_{2,1} + 11.7046999107196 q_{1,4} q_{2,2} + 38.2753184180093 q_{1,4} q_{2,3} + 35.1710107901379 q_{2,0} q_{3,1} + 16.2788205960997 q_{2,0} q_{3,2} + 36.0693775937429 q_{2,0} q_{3,3} + 8.60232526704263 q_{2,0} q_{3,4} + 35.1710107901379 q_{2,1} q_{3,0} + 37.6563407675255 q_{2,1} q_{3,2} + 19.2353840616713 q_{2,1} q_{3,3} + 41.194659848092 q_{2,1} q_{3,4} + 16.2788205960997 q_{2,2} q_{3,0} + 37.6563407675255 q_{2,2} q_{3,1} + 29.732137494637 q_{2,2} q_{3,3} + 11.7046999107196 q_{2,2} q_{3,4} + 36.0693775937429 q_{2,3} q_{3,0} + 19.2353840616713 q_{2,3} q_{3,1} + 29.732137494637 q_{2,3} q_{3,2} + 38.2753184180093 q_{2,3} q_{3,4} + 8.60232526704263 q_{2,4} q_{3,0} + 41.194659848092 q_{2,4} q_{3,1} + 11.7046999107196 q_{2,4} q_{3,2} + 38.2753184180093 q_{2,4} q_{3,3} + 35.1710107901379 q_{3,0} q_{4,1} + 16.2788205960997 q_{3,0} q_{4,2} + 36.0693775937429 q_{3,0} q_{4,3} + 8.60232526704263 q_{3,0} q_{4,4} + 35.1710107901379 q_{3,1} q_{4,0} + 37.6563407675255 q_{3,1} q_{4,2} + 19.2353840616713 q_{3,1} q_{4,3} + 41.194659848092 q_{3,1} q_{4,4} + 16.2788205960997 q_{3,2} q_{4,0} + 37.6563407675255 q_{3,2} q_{4,1} + 29.732137494637 q_{3,2} q_{4,3} + 11.7046999107196 q_{3,2} q_{4,4} + 36.0693775937429 q_{3,3} q_{4,0} + 19.2353840616713 q_{3,3} q_{4,1} + 29.732137494637 q_{3,3} q_{4,2} + 38.2753184180093 q_{3,3} q_{4,4} + 8.60232526704263 q_{3,4} q_{4,0} + 41.194659848092 q_{3,4} q_{4,1} + 11.7046999107196 q_{3,4} q_{4,2} + 38.2753184180093 q_{3,4} q_{4,3}
組合せ最適化モデルの作成 ¶
制約条件の作成、目的関数の作成 で作成した目的関数と制約条件を組み合わせて、組合せ最適化のモデルを作成します。
model = route_length + (constraints2 + constraints3) * np.max(distance)
print(model)
minimize:
35.1710107901379 q_{0,0} q_{1,1} + 16.2788205960997 q_{0,0} q_{1,2} + 36.0693775937429 q_{0,0} q_{1,3} + 8.60232526704263 q_{0,0} q_{1,4} + 35.1710107901379 q_{0,0} q_{4,1} + 16.2788205960997 q_{0,0} q_{4,2} + 36.0693775937429 q_{0,0} q_{4,3} + 8.60232526704263 q_{0,0} q_{4,4} + 35.1710107901379 q_{0,1} q_{1,0} + 37.6563407675255 q_{0,1} q_{1,2} + 19.2353840616713 q_{0,1} q_{1,3} + 41.194659848092 q_{0,1} q_{1,4} + 35.1710107901379 q_{0,1} q_{4,0} + 37.6563407675255 q_{0,1} q_{4,2} + 19.2353840616713 q_{0,1} q_{4,3} + 41.194659848092 q_{0,1} q_{4,4} + 16.2788205960997 q_{0,2} q_{1,0} + 37.6563407675255 q_{0,2} q_{1,1} + 29.732137494637 q_{0,2} q_{1,3} + 11.7046999107196 q_{0,2} q_{1,4} + 16.2788205960997 q_{0,2} q_{4,0} + 37.6563407675255 q_{0,2} q_{4,1} + 29.732137494637 q_{0,2} q_{4,3} + 11.7046999107196 q_{0,2} q_{4,4} + 36.0693775937429 q_{0,3} q_{1,0} + 19.2353840616713 q_{0,3} q_{1,1} + 29.732137494637 q_{0,3} q_{1,2} + 38.2753184180093 q_{0,3} q_{1,4} + 36.0693775937429 q_{0,3} q_{4,0} + 19.2353840616713 q_{0,3} q_{4,1} + 29.732137494637 q_{0,3} q_{4,2} + 38.2753184180093 q_{0,3} q_{4,4} + 8.60232526704263 q_{0,4} q_{1,0} + 41.194659848092 q_{0,4} q_{1,1} + 11.7046999107196 q_{0,4} q_{1,2} + 38.2753184180093 q_{0,4} q_{1,3} + 8.60232526704263 q_{0,4} q_{4,0} + 41.194659848092 q_{0,4} q_{4,1} + 11.7046999107196 q_{0,4} q_{4,2} + 38.2753184180093 q_{0,4} q_{4,3} + 35.1710107901379 q_{1,0} q_{2,1} + 16.2788205960997 q_{1,0} q_{2,2} + 36.0693775937429 q_{1,0} q_{2,3} + 8.60232526704263 q_{1,0} q_{2,4} + 35.1710107901379 q_{1,1} q_{2,0} + 37.6563407675255 q_{1,1} q_{2,2} + 19.2353840616713 q_{1,1} q_{2,3} + 41.194659848092 q_{1,1} q_{2,4} + 16.2788205960997 q_{1,2} q_{2,0} + 37.6563407675255 q_{1,2} q_{2,1} + 29.732137494637 q_{1,2} q_{2,3} + 11.7046999107196 q_{1,2} q_{2,4} + 36.0693775937429 q_{1,3} q_{2,0} + 19.2353840616713 q_{1,3} q_{2,1} + 29.732137494637 q_{1,3} q_{2,2} + 38.2753184180093 q_{1,3} q_{2,4} + 8.60232526704263 q_{1,4} q_{2,0} + 41.194659848092 q_{1,4} q_{2,1} + 11.7046999107196 q_{1,4} q_{2,2} + 38.2753184180093 q_{1,4} q_{2,3} + 35.1710107901379 q_{2,0} q_{3,1} + 16.2788205960997 q_{2,0} q_{3,2} + 36.0693775937429 q_{2,0} q_{3,3} + 8.60232526704263 q_{2,0} q_{3,4} + 35.1710107901379 q_{2,1} q_{3,0} + 37.6563407675255 q_{2,1} q_{3,2} + 19.2353840616713 q_{2,1} q_{3,3} + 41.194659848092 q_{2,1} q_{3,4} + 16.2788205960997 q_{2,2} q_{3,0} + 37.6563407675255 q_{2,2} q_{3,1} + 29.732137494637 q_{2,2} q_{3,3} + 11.7046999107196 q_{2,2} q_{3,4} + 36.0693775937429 q_{2,3} q_{3,0} + 19.2353840616713 q_{2,3} q_{3,1} + 29.732137494637 q_{2,3} q_{3,2} + 38.2753184180093 q_{2,3} q_{3,4} + 8.60232526704263 q_{2,4} q_{3,0} + 41.194659848092 q_{2,4} q_{3,1} + 11.7046999107196 q_{2,4} q_{3,2} + 38.2753184180093 q_{2,4} q_{3,3} + 35.1710107901379 q_{3,0} q_{4,1} + 16.2788205960997 q_{3,0} q_{4,2} + 36.0693775937429 q_{3,0} q_{4,3} + 8.60232526704263 q_{3,0} q_{4,4} + 35.1710107901379 q_{3,1} q_{4,0} + 37.6563407675255 q_{3,1} q_{4,2} + 19.2353840616713 q_{3,1} q_{4,3} + 41.194659848092 q_{3,1} q_{4,4} + 16.2788205960997 q_{3,2} q_{4,0} + 37.6563407675255 q_{3,2} q_{4,1} + 29.732137494637 q_{3,2} q_{4,3} + 11.7046999107196 q_{3,2} q_{4,4} + 36.0693775937429 q_{3,3} q_{4,0} + 19.2353840616713 q_{3,3} q_{4,1} + 29.732137494637 q_{3,3} q_{4,2} + 38.2753184180093 q_{3,3} q_{4,4} + 8.60232526704263 q_{3,4} q_{4,0} + 41.194659848092 q_{3,4} q_{4,1} + 11.7046999107196 q_{3,4} q_{4,2} + 38.2753184180093 q_{3,4} q_{4,3}
subject to:
q_{0,0} + q_{0,1} + q_{0,2} + q_{0,3} + q_{0,4} == 1 (weight: 41.19465984809196),
q_{1,0} + q_{1,1} + q_{1,2} + q_{1,3} + q_{1,4} == 1 (weight: 41.19465984809196),
q_{2,0} + q_{2,1} + q_{2,2} + q_{2,3} + q_{2,4} == 1 (weight: 41.19465984809196),
q_{3,0} + q_{3,1} + q_{3,2} + q_{3,3} + q_{3,4} == 1 (weight: 41.19465984809196),
q_{4,0} + q_{4,1} + q_{4,2} + q_{4,3} + q_{4,4} == 1 (weight: 41.19465984809196),
q_{0,0} + q_{1,0} + q_{2,0} + q_{3,0} + q_{4,0} == 1 (weight: 41.19465984809196),
q_{0,1} + q_{1,1} + q_{2,1} + q_{3,1} + q_{4,1} == 1 (weight: 41.19465984809196),
q_{0,2} + q_{1,2} + q_{2,2} + q_{3,2} + q_{4,2} == 1 (weight: 41.19465984809196),
q_{0,3} + q_{1,3} + q_{2,3} + q_{3,3} + q_{4,3} == 1 (weight: 41.19465984809196),
q_{0,4} + q_{1,4} + q_{2,4} + q_{3,4} + q_{4,4} == 1 (weight: 41.19465984809196)
制約条件に距離行列の最大値をかけているのは、制約条件に重みをつけるためです。今回使用するソルバーである Amplify AE においては、制約条件に適切な重みを指定しないと、ソルバーが制約条件をみたそうとするよりも目的関数を小さくする方向に動いてしまい、良い解を発見することができなくなってしまいます。詳しくは 制約条件とペナルティ関数 を参照してください。
ソルバークライアントの作成 ¶
ソルバークライアントを作成し、求解を行うためのソルバーの指定およびソルバーのパラメータの設定を行います。Amplify SDK はさまざまなソルバーに対応していますが、本サンプルコードでは Amplify AE を使用します。Amplify AE に対応するソルバークライアントクラスは FixstarsClient クラスです。
from amplify import FixstarsClient
client = FixstarsClient()
Amplify AE の実行に必要な API トークンを設定します。
Tip
ユーザ登録を行うと、評価・検証目的に使える API トークンを無料で入手できます。
client.token = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
ソルバーのタイムアウト値を設定します。Amplify AE のタイムアウト値の単位は ms ですが、タイムアウト値の単位はソルバーによって様々なため、datetime モジュールを使用して統一的にタイムアウト値を指定できます。
import datetime
client.parameters.timeout = datetime.timedelta(seconds=1)
これでソルバーの設定は完了です。
求解の実行 ¶
作成した組合せ最適化モデルとソルバークライアントを使用してソルバーの実行を行い、巡回セールスマン問題の解を求めます。
from amplify import solve
result = solve(model, client)
目的関数の値、つまり巡回路の長さは以下のように表示できます。
result.best.objective
104.44555752420855
最適解における変数の値は、NumPy の多次元配列の形式で以下のようにして取得できます。
q_values = q.evaluate(result.best.values)
print(q_values)
[[0. 0. 0. 0. 1.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0.]
[0. 1. 0. 0. 0.]
[1. 0. 0. 0. 0.]
[0. 0. 0. 0. 1.]]
結果の確認¶
Amplify SDK のチュートリアルとしては以上で十分ですが、結果が正しそうであることを可視化しておきます。
import matplotlib.pyplot as plt
%matplotlib inline
まず、都市の位置を可視化します。
plt.scatter(x, y)
plt.show()
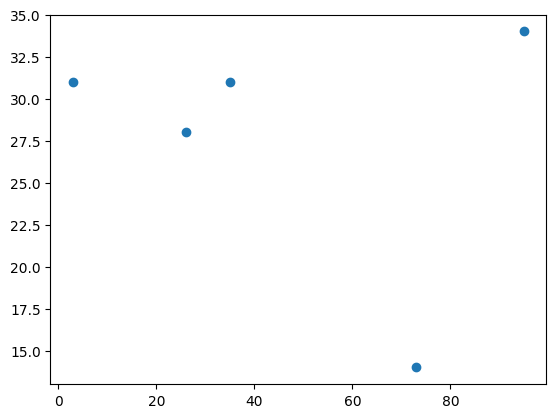
次に、巡回路を可視化します。q_values は置換行列 (の最後に 1 行足したもの) と見なせるので、各都市を順に並べたベクトルに q_values を左から掛けることにより、巡回路で訪問する順に並び替えることができます。
route_x = q_values @ x # 移動ルートの x 座標を取得
route_y = q_values @ y # 移動ルートの y 座標を取得
plt.scatter(x, y)
plt.plot(route_x, route_y)
plt.show()
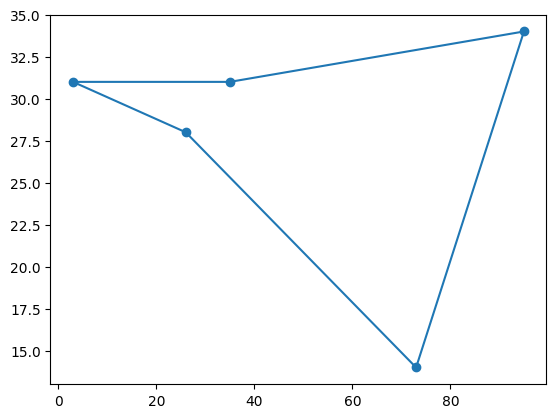
最短路が求められていることが分かります。