グラフ埋め込み¶

QUBO ソルバーやイジングソルバーの中には、任意の 2 次多項式を受け取れず、入力できる 2 次の項が制限されているものもあります。Amplify SDK は、そのようなソルバーに対して、グラフ埋め込みとよばれる操作を行い、多項式をそのソルバーが受け取れる形に変換します。

グラフ埋め込みが必要なソルバーの代表例は D-Wave のマシンです。D-Wave マシンの QPU には、マシンごとに異なる量子ビット間の物理的なトポロジーが存在するため、この量子ビット間の結合をグラフ構造と見立てた場合に、入力できる二次多項式の項はこのグラフ構造に制限されます。このグラフ構造を物理グラフと呼び、Amplify SDK が構築する中間モデルの多項式のグラフ構造を中間グラフと呼びます。グラフ埋め込みとは、中間グラフを物理グラフに埋め込む操作のことを指します。

参考

グラフ埋め込みが必要なソルバーは、こちらのページで Graph タグがついているソルバーです。

D-Wave マシンの QPU のトポロジーについては D-Wave QPU Architecture: Topologies を参照してください。

グラフ埋め込みとは¶

埋め込みが必要なソルバーは、入力できる 2 次項の種類が限られています。つまり、あるインデックスのペアの集合 \(E\) があって、入力する多項式に含まれる 2 次項はすべて

\[ c_{ab} q_a q_b \quad (c_{ab} \in \mathbb{R}, (a, b) \in E) \]

と表せる必要があります。\(E\) は通常、変数をノードとみなし、入力できる 2 次の項に含まれる 2 つの変数をエッジでつないだグラフとして表されます。

また、入力したい多項式に対しても、その多項式に含まれる 2 次の項それぞれに注目し、その 2 つの変数をエッジでつないだグラフを考えることができます。

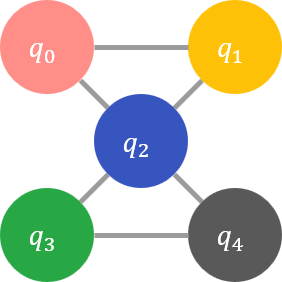
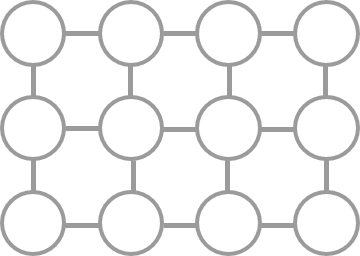
たとえば、目的関数が \(q_0 q_1 + 2 q_1 q_2 - 3 q_0 q_2 + 4 q_2 q_3 - 5 q_3 q_4 - 6 q_2 q_4\) で、ソルバーに入力できる 2 次項を表すグラフ \(E\) が \(3 \times 4\) の格子グラフである場合、目的関数を変換したグラフ \(P\) および \(E\) はそれぞれ以下の図のようになります。

ここで、\(P\) の各変数を \(E\) のノードのうちいくつかに割り当てて、以下の条件をみたすように \(P\) と \(E\) 上のノードの対応関係を求める操作を グラフ埋め込み と呼びます。

どの \(P\) の変数 \(q_i\) に対しても、対応する \(E\) のノードが一つ以上存在する (1対多の割り当てが許される)
どの \(E\) のノード \(a\) に対しても、対応する \(P\) の変数はたかだか一つである (割り当てに重複が無い)
\(P\) 上で \(q_i\) と \(q_j\) が隣り合っているとき、\(q_i\) と \(q_j\) それぞれに対応し \(E\) 上のどこかで隣り合う \(E\) のノード \(a\) と \(b\) が存在する
すべての \(P\) の変数 \(q_i\) について \(q_i\) に対応する \(E\) のノード \(a\) からなる \(E\) の部分グラフは連結である (チェインと呼ぶ)

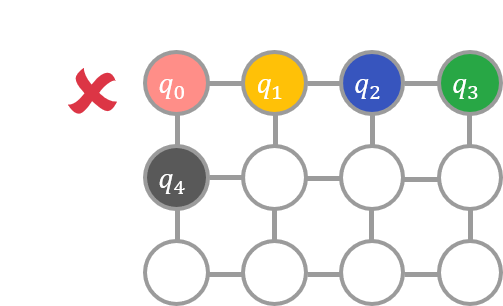
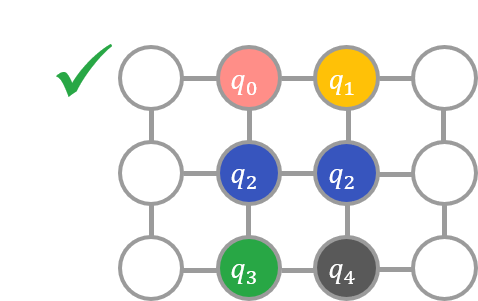
たとえば、以下の左の図のように \(E\) に適当に変数を割り当ててしまうと、\(q_0\) が割り当てられているノードと \(q_2\) が割り当てられているノードが隣り合っていないので条件をみたしません。一方で、以下の 2 番目の図のように変数を割り当てると条件が満たされます。

グラフ埋め込みに成功した場合、目的関数を以下のようにしてソルバーが受け取れる形に変換できます。

グラフ埋め込みによる多項式の変換

目的関数の 2 次の項: 目的関数の 2 次の項 \(Q_{ij} q_i q_j\) を \(\sum_{a,b} c_{ab} q_a q_b \left( Q_{ij} = \sum_{a,b} c_{ab} \right)\) となるように変換して新たな目的関数に加算する。ここで \(q_a\) は \(q_i\) が割り当てられた \(E\) のノード \(a\) の変数、\(q_b\) は \(q_j\) が割り当てられた \(E\) のノード \(b\) の変数で、 \(a\) と \(b\) は隣接している。
目的関数の 1 次の項: 目的関数の 1 次の項 \(Q_{ii} q_i\) を \(\sum_{a} c_{aa} q_a \left( Q_{ii} = \sum_{a} c_{aa} \right)\) となるように変換して新たな目的関数に加算する。ここで \(q_a\) は \(q_i\) が割り当てられた \(E\) のノード \(a\) の変数とする。
目的関数の定数項: 新たな目的関数にそのまま加算する。

チェイン制約

\(P\) の変数 \(q_i\) に対応する全ての \(E\) のノード \(a\) からなる部分グラフについて、隣り合うノード上の変数 \(q_{a}\) と \(q_{a'}\) が \(q_{a} = q_{a'}\) となる制約を満たすようにペナルティ関数を加算する。

1つのチェインに対するペナルティ関数は次のように与えられます。

バイナリ変数 \(q\) の場合:

\[ \sum_{a, a'} \left( q_a - q_{a'} \right)^2 \]

イジング変数 \(s\) の場合:

\[ - \frac{1}{2} \sum_{a, a'} s_a s_{a'} \]

必要なペナルティ関数の重みは \(q_i\) の係数に依存します。これをチェイン強度と呼びます。

ソルバーの実行結果はグラフ \(E\) 上の変数に対するものになります。そのため、グラフ埋め込みの逆変換を行い元のグラフ \(P\) 上の変数の値を決定しなくてはなりません。グラフ \(P\) の変数 \(q_i\) に対応するグラフ \(E\) の変数 \(q_a\) は複数存在します。理想的には全ての変数の値 \(q_a\) が同じになることですが、実際には異なる値がソルバーから返されることもあります。そのような状況をチェインが壊れていると表現し、ある物理グラフ上の多項式に対してチェインが壊れている割合を chain break fraction と呼びます。壊れているチェインについて \(q_i\) が二値変数の場合「多数決」によって決定されることが多いです。

グラフ埋め込み処理¶

solve() 関数の内部では中間モデルの構築後に、必要に応じて自動的にグラフ埋め込みが行われ、その後ソルバーの実行を行います。ここからは Amplify SDK が solve() 関数の内部で行っているグラフ埋め込み処理について、ステップごとに詳しく説明します。

以下では、\(4 \times 4\) 変数のバイナリ変数からなる目的関数と制約条件を持つモデルに対して DWaveSamplerClient を対象にグラフ埋め込みを行う例を示します。

from amplify import DWaveSamplerClient, VariableGenerator, Model, equal_to, to_edges
import numpy as np

# 変数の生成
gen = VariableGenerator()
q = gen.array("Binary", shape=(4, 4))

# 目的関数と制約条件の定義
rng = np.random.default_rng()
p = (q[:-1] * q[1:] * rng.uniform(-1, 1, (3, 4))).sum()
c = equal_to(q, 1, axis=1)

# 入力モデルの作成
m = p + c

# ソルバークライアントの作成
client = DWaveSamplerClient()

多項式からグラフへの変換¶

まず、to_intermediate_model() メソッドを用いて中間モデルを取得します。今回のモデルは二次バイナリ変数で構成されているためこの操作は必須ではないですが、変数変換や次数下げを行う場合は必要になります。

im, im_mapping = m.to_intermediate_model(client.acceptable_degrees)

次に、DWaveSamplerClient は制約条件を扱うことができないため、目的関数に全ての制約条件のペナルティを足し合わせた多項式を計算します。

im_unconstrained = im.to_unconstrained_poly()

これでバイナリ変数の二次多項式として中間モデルを取得できました。二次多項式のグラフ表現は to_edges 関数を用いて取得できます。グラフのノードを変数の id で表したとき、この関数はエッジを id のタプルのリストで返却します。1 次の項は自己ループとして表されます。

edges = to_edges(im_unconstrained)

>>> im_unconstrained.variables
[Variable({name: q_{0,0}, id: 0, type: Binary}),
 Variable({name: q_{0,1}, id: 1, type: Binary}),
 Variable({name: q_{0,2}, id: 2, type: Binary}),
 ...
]
>>> edges
[(0, 4), (1, 5), (2, 6), (3, 7), (4, 8), (5, 9), (6, 10), ...]

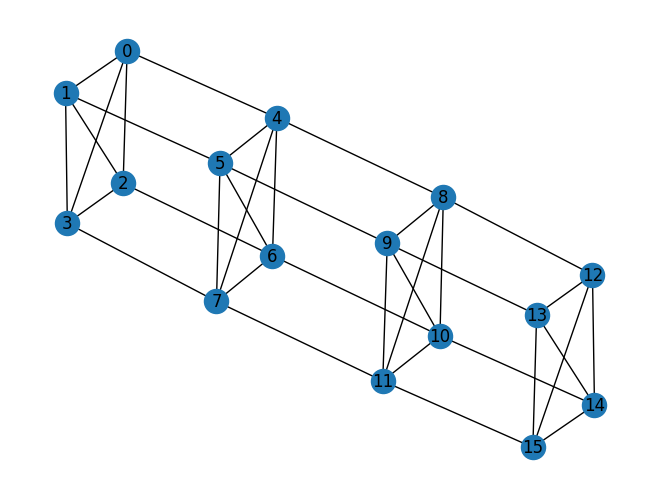
次のようにして networkx モジュールを用いてグラフを可視化することができます。

import networkx as nx

g = nx.Graph()
g.add_edges_from(edges)
g.remove_edges_from(nx.selfloop_edges(g))
nx.draw(g, with_labels=True)

_images/898c0b33dd8134fe89b589a701a224ba6abc550f9a52a2067d672ec81d76f9ef.png

物理グラフの取得¶

グラフ埋め込みが必要なソルバークライアントクラスには、graph アトリビュートがあります。これは Graph クラスのインスタンスであり、ソルバーの物理グラフを表します。Graph クラスは次のアトリビュートを持ちます。

アトリビュート	データ型	詳細
`type`	`str`	グラフの種類
`shape`	`list`[`int`]	グラフのサイズパラメータ
`nodes`	`list`[`int`]	グラフに含まれるノードのリスト
`edges`	`list`[`tuple`[`int`, `int`]]	グラフのエッジのリスト
`adjacency`	`list`[`list`[`int`]]	ノードごとの隣接ノードのリスト

DWaveSamplerClient を例として、graph アトリビュートを取得します。

from amplify import DWaveSamplerClient

client = DWaveSamplerClient()
client.solver = "Advantage_system4.1"
graph = client.graph

>>> graph.type
'Pegasus'
>>> graph.shape
[16]
>>> len(graph.nodes)
5627
>>> len(graph.edges)
40279

物理グラフは、 networkx モジュールを用いて edges を描画することで可視化できます。一方で、dwave_networkx モジュールを用いると shape に応じた整ったレイアウトでグラフを描画できます。次の図は、ペガサスグラフ (shape=4) をプロットする例です。

import dwave_networkx as dnx

p = dnx.pegasus_graph(4)
dnx.draw_pegasus(p, with_labels=True)

_images/279ae0b3bc5c5637e1e991d9c30dd7a4a46172c8ecb79b6096cd7f3886fb437b.png — ペガサスグラフ (`shape=4`)¶

グラフ埋め込みの実行¶

グラフ埋め込みを実行して埋め込みの情報を取得するには、embed() 関数を呼び出します。この関数は多項式 Poly と Graph クラスのインスタンスを引数に取り、グラフ埋め込み後の多項式とグラフ埋め込みのマッピング、引数の多項式をグラフに変換したものからなるタプルを返します。

from amplify import embed

# D-Wave のグラフに対してグラフ埋め込みを行う
emb_poly, embedding, src_graph = embed(im_unconstrained, graph)

emb_poly にはグラフ埋め込みによる多項式の変換が行われた多項式が返却されます。embedding は im_unconstrained に使われている変数の id から、emb_poly に現れる変数の id へのマッピング (チェイン) を表すリストです。リストのインデックスは im_unconstrained に使われている変数の id に対応します。

>>> embedding
[array([ 180,  181, 2940], dtype=uint32),
 array([ 195,  196, 2955], dtype=uint32),
 array([ 150,  151, 2970], dtype=uint32),
 array([ 165,  166, 2985], dtype=uint32),
 ...]

src_graph は im_unconstrained のグラフ表現です。im_unconstrained に to_edges 関数を適用した場合と同じ結果が返ります。

次のように dwave_networkx モジュールを用いてグラフ埋め込みを可視化できます。

p = dnx.pegasus_graph(*graph.shape)
dnx.draw_pegasus_embedding(
    p,
    emb={i: v.tolist() for i, v in enumerate(embedding)},
    embedded_graph=g,
    show_labels=True
)

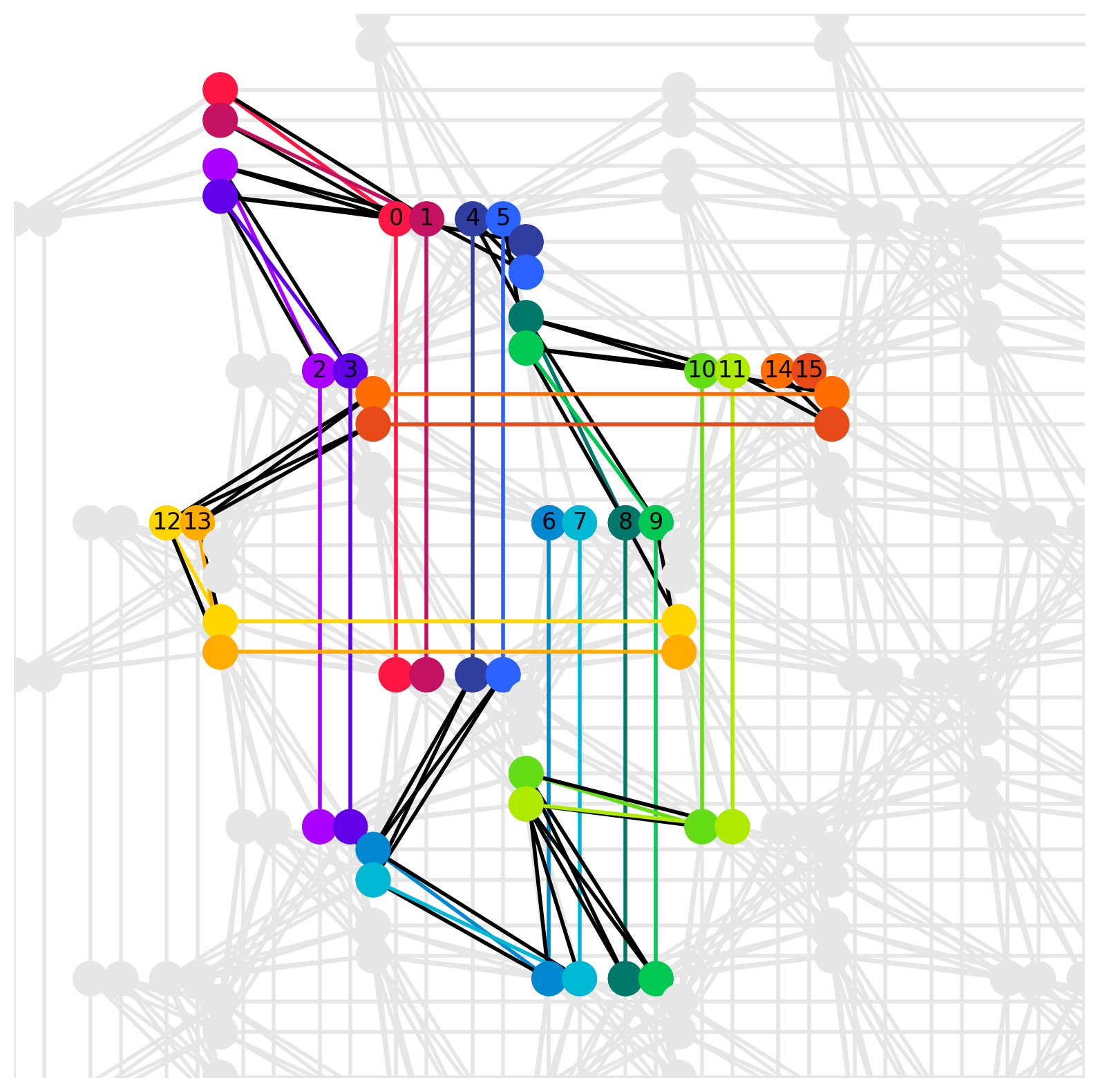
_images/e69612b85c6db44301bf84a91ab892ddc5ab309a0fbf2772b997cc952158c45f.png — ペガサスグラフ (`shape=16`) へのグラフ埋め込み例¶

上の図で、ノードに書かれた番号は埋め込み前の多項式 im_unconstrained の変数の id を表します。同じ色で繋がった複数のノードはチェインを表し、埋め込み前の 1 つの変数に対応します。また、異なる色のノード同士を結ぶ黒い線は、埋め込み前の多項式 im_unconstrained に含まれる 2 次の項に対応する物理グラフ上のエッジを表します。

グラフ埋め込みの実行パラメータ¶

グラフ埋め込みの実行に関する以下のパラメータが提供されています。埋め込みの実行パラメータは、solve() 関数および embed() 関数のキーワード引数として指定することができます。

パラメータ	説明
`embedding_timeout`	グラフ埋め込み探索のタイムアウト
`embedding_method`	グラフ埋め込みに使用するアルゴリズム
`chain_strength`	目的関数に足されるチェインペナルティの重み

埋め込みのタイムアウト¶

solve() 関数または embed() 関数の embedding_timeout キーワード引数に数値または datetime.timedelta オブジェクトを与えることで、グラフ埋め込みに使用する時間のタイムアウトを指定することができます。デフォルトは 10 秒です。

埋め込みのアルゴリズム¶

以下のアルゴリズムが提供されています。埋め込みアルゴリズムを指定したい場合は、solve() 関数または embed() 関数の embedding_method キーワード引数に指定します。

Clique

埋め込み対象のグラフのノード数と同一の全結合グラフの埋め込みを探索します。

一度探索されたクリーク埋め込みはキャッシュ化されます。対象のグラフのノード数のみに依存するためキャッシュを利用した高速な探索が可能なことがあります。しかし、クリーク埋め込みが可能な最大ノード数は物理グラフのみで決まるため、本質的に埋め込みが可能なノード数を超えるグラフでは必ず失敗します。

Minor

minorminer を用いたマイナー埋め込みを行います。

対象のグラフが疎であれば、Clique 埋め込みより効率の良い (チェインの短い) 埋め込みが期待出来ることや、Clique 埋め込みが失敗するようなサイズの入力に対してもマイナー埋め込みなら成功する可能性があります。

探索のタイムアウト時間は embedding_timeout キーワード引数で指定します。

Default (Default)

最初に Clique 埋め込みを試みて、失敗した場合は Minor 埋め込みに切り替えます。

Parallel

Clique 埋め込みと Minor 埋め込みを並列に実行し、チェインの変数の数が少ない方の結果を選択します。

チェイン強度¶

目的関数をグラフ埋め込みに応じて変換するとき、同じ入力変数に割り当てられたノードがすべて同じ値をとるようにチェイン制約がかけられます。Amplify SDK は自動でチェイン制約のペナルティを埋め込み後の多項式に追加しますが、この時のペナルティの重みの初期値は、埋め込み前の多項式の 2 次の係数の二乗平均平方根を変数の数で割ったものになります。solve() 関数または embed() 関数の chain_strength キーワード引数を与えることで、このペナルティの相対的な重みを設定することができます。デフォルトは 1.0 です。

重要

上記の二乗平均平方根による初期値の設定は D-Wave の実装に基づくものです。Amplify SDK での計算方法は将来的に変更される可能性があります。

ソルバーの実行結果とグラフ変換¶

Amplify SDK はグラフ埋め込みが必要なソルバーが指定された場合、solve() 関数内でグラフ埋め込みを行います。どのような埋め込みが行われたかの情報は、solve() 関数が返す Result クラスの embedding アトリビュートに GraphConversion クラスのインスタンスとして格納されます。

注釈

グラフ埋め込みが不要なソルバーに対しては、embedding アトリビュートは None を返すことに注意してください。

GraphConversion クラスは以下のアトリビュートを持ちます。

アトリビュート	データ型	詳細
`src_graph`	`list`[`tuple`[`int`, `int`]]	中間モデルの目的関数と制約条件のペナルティを足した多項式のグラフの表現
`dst_graph`	`Graph`	ソルバー固有の物理グラフ
`chains`	`list`[`numpy.ndarray`]	中間モデルの変数の `id` と物理グラフ上の変数の `id` の対応を表すリスト
`poly`	`Poly`	中間モデルの多項式に対してグラフ埋め込みを行った結果の多項式
`num_variables`	`int`	`poly` の変数の数
`values_list`	`ValuesList`	ソルバーが返した解
`chain_break_fractions`	`ChainBreakFractions`	ソルバーが返した各々の解においてチェインが壊れている割合

例として、次のモデルに対して DWaveSamplerClient を用いて solve() 関数を実行した結果から、グラフ埋め込みの情報を取得します。

from amplify import VariableGenerator, Model, DWaveSamplerClient, solve

gen = VariableGenerator()
q = gen.array("Binary", 3)

objective = q[0] * q[1] + 2 * q[1] * q[2] - 3 * q[0] * q[2]
model = Model(objective)

client = DWaveSamplerClient()
client.token = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"

result = solve(model, client)

src_graph アトリビュートにより、中間モデルのペナルティ関数込みの多項式をエッジのリストに変換したものが取得できます。

>>> result.embedding.src_graph
[(0, 1), (1, 2), (0, 2)]

中間モデルの多項式に含まれる変数の id は以下のようにして調べることができます。

>>> im_unconstrained = result.intermediate.model.to_unconstrained_poly()
>>> print(im_unconstrained)
q_0 q_1 - 3 q_0 q_2 + 2 q_1 q_2
>>> im_unconstrained.variables
[Variable({name: q_0, id: 0, type: Binary}),
 Variable({name: q_1, id: 1, type: Binary}),
 Variable({name: q_2, id: 2, type: Binary})]

dst_graph アトリビュートは、物理グラフとしてソルバークライアントの graph アトリビュートと同一の Graph クラスのインスタンスを返します。

>>> result.embedding.dst_graph.type
'Pegasus'
>>> result.embedding.dst_graph.shape
[16]

chains アトリビュートは、中間レイヤの変数とソルバーの変数の間のマッピングを表します。chains はチェインのリストとして表され、各チェインは 1 次元の ndarray オブジェクトとして表されます。たとえば以下の例では、中間レイヤの 0 番目の変数は 2940 番の変数のみに対応することが分かります。

>>> result.embedding.chains
[array([2940], dtype=uint32), array([2955], dtype=uint32), array([45], dtype=uint32)]
>>> print(result.embedding.chains[0])
[2940]

poly アトリビュートからグラフ埋め込み後の多項式が取得できます。これは実際にソルバーに入力された多項式と同一のものです。

>>> print(result.embedding.poly)
- 3 q_{45} q_{2940} + 2 q_{45} q_{2955} + q_{2940} q_{2955}

num_variables アトリビュートは、poly アトリビュートに含まれる変数の数を表します。問題の簡単さを表す 1 つの指標として使うことができ、一般的には、この値が小さいほど解きやすい問題であるといえます。

>>> result.embedding.num_variables
3

values_list アトリビュートによりソルバーが返した解の値のリストを取得できます。これはソルバーが返した解の個数と同じ長さを持つ list ライクなオブジェクトで、それぞれの要素はソルバーが返した解に対応します。解は辞書として表現され、キーはソルバーの変数です。

>>> print(result.embedding.values_list)
[{q_{45}: 1, q_{2940}: 1, q_{2955}: 0}]

chain_break_fractions アトリビュートは、ソルバーが返したそれぞれの解について、チェイン制約が壊れている割合を表します。適切な値は一般に問題によって異なり、必ずしも 0 である必要は無いと考えられています。もし、この値が大き過ぎることで良い解が得られない場合には、solve() 関数の chain_strength キーワード引数に 1.0 より大きな値を与え、逆に小さすぎる場合には 1.0 より小さな値を与えることで、性能が改善することがあります。

>>> print(result.embedding.chain_break_fractions)
[0]

Tip

solve() 関数が返す Result オブジェクトに解が含まれていない場合、Result オブジェクトの filter_solution プロパティを False に指定することでソルバーが返した解をすべて取得することができます。詳しくは解のフィルターを参照してください。