二次割当問題

二次割当問題は、以下のような問題です。

二次割当問題

\(N\) を正の整数とする。\(N\) 個の工場建設候補地に \(N\) 個の工場を建設することを考える。それぞれの工場は、どの建設候補地に建設されても良い。どの 2 つの工場にも、それらを行き来するトラックが走っており、その輸送量はあらかじめ分かっている。輸送量 x 走行距離の和を最小化するにはどうすればよいか。

応用として、集会の座席表を仲が良い人同士が近くなるように決定することなどが考えられます。

定式化

\(N\) 個の工場建設候補地を 土地 \(0\), 土地 \(1\), ..., 土地 \(N-1\) と表記し、\(N\) 個の工場を工場 \(0\), 工場 \(1\), ..., 工場 \(N-1\) と表記します。また土地 \(i\) と土地 \(j\) の距離を \(D_{i, j}\), 工場 \(k\) と工場 \(l\) の間の輸送量を \(F_{k, l}\) とします。

変数

\(N \times N\) 個のバイナリ変数 \(q\) を用意し、\(q_{i, k}\) は工場 \(k\) を土地 \(i\) に建設するかどうかを表すことにします。

たとえば、\(q\) が以下のような値をとるとき、土地 \(0\) には 工場 \(3\) が建設されます。

バイナリ変数テーブル

	工場 0	工場 1	工場 2	工場 3	工場 4
土地 0	0	0	0	1	0
土地 1	0	1	0	0	0
土地 2	0	0	0	0	1
土地 3	1	0	0	0	0
土地 4	0	0	1	0	0

制約条件

バイナリ変数テーブルのそれぞれの行と列には 1 となる値がちょうど 1 個である必要があります。したがって、各行各列に one-hot 制約をかけます。逆に、これらがみたされていれば、どの土地にどの工場を建設するかが 1 通りに定まります。

目的関数

目的関数は、工場と工場の間の輸送量 x 距離の総和です。これは \(q\) を用いて数式で表すと

\[ \sum_{q_{i, k} = 1, q_{j, l} = 1} D_{i, j} \ F_{k, l} = \sum_{i, j, k, l} q_{i, k} \ q_{j, l} \ D_{i, j} \ F_{k, l} \]

となります。

数式

以上の定式化は、\(N\times N\) 個のバイナリ変数 \(q\) を用いて

\[\begin{split} \begin{align} \text{minimize} \quad &\sum_{i, j, k, l} q_{i, k} \ q_{j, l} \ D_{i, j} \ F_{k, l} \\ \text{subject to} \quad &\sum_k q_{i, k} = 1 \quad \text{for} \quad i \in \{0, 1, \ldots, N - 1\}, \\ &\sum_i q_{i, k} = 1 \quad \text{for} \quad k \in \{0, 1, \ldots, N - 1\}, \\ &q_{i, k} \in \{0, 1\} \quad \text{for} \quad i, k \in \{0, 1, \ldots, N - 1\} \end{align} \end{split}\]

と書くことができます。

問題の作成

Amplify SDK による定式化を行う前に、問題を作成しておきます。簡単のため工場の数 \(N\) を 10 とします。

import numpy as np

N = 10

土地間の距離を表す行列 \(D\) を作成します。土地はユークリッド平面上にランダムに生成します。距離行列は 2 次元の numpy.ndarray として作成します。名前は distance とします。

rng = np.random.default_rng()

x = rng.integers(0, 100, size=(N,))
y = rng.integers(0, 100, size=(N,))

distance = (
    (x[:, np.newaxis] - x[np.newaxis, :]) ** 2
    + (y[:, np.newaxis] - y[np.newaxis, :]) ** 2
) ** 0.5

print(distance)

[[ 0.         34.82814953 41.10960958 11.         38.05259518 69.02897942
  50.08991915 89.55445271 37.85498646 76.57675888]
 [34.82814953  0.         22.02271555 29.15475947 29.68164416 53.23532662
  41.03656906 60.67124525 38.07886553 85.        ]
 [41.10960958 22.02271555  0.         30.87069808 11.04536102 31.95309062
  19.41648784 48.76474136 21.09502311 65.80273551]
 [11.         29.15475947 30.87069808  0.         27.07397274 58.03447251
  39.11521443 79.60527621 27.20294102 68.62215386]
 [38.05259518 29.68164416 11.04536102 27.07397274  0.         31.
  13.         55.6057551  10.04987562 55.71355311]
 [69.02897942 53.23532662 31.95309062 58.03447251 31.          0.
  19.6468827  36.40054945 33.52610923 53.15072906]
 [50.08991915 41.03656906 19.41648784 39.11521443 13.         19.6468827
   0.         50.44799302 13.92838828 47.67598976]
 [89.55445271 60.67124525 48.76474136 79.60527621 55.6057551  36.40054945
  50.44799302  0.         62.93647591 89.28605714]
 [37.85498646 38.07886553 21.09502311 27.20294102 10.04987562 33.52610923
  13.92838828 62.93647591  0.         46.95742753]
 [76.57675888 85.         65.80273551 68.62215386 55.71355311 53.15072906
  47.67598976 89.28605714 46.95742753  0.        ]]

工場間の輸送量を表す行列 \(F\) を作成します。2 次元の対称行列をランダムに作成し、名前は flow とします。

flow = np.zeros((N, N), dtype=int)
for i in range(N):
    for j in range(i + 1, N):
        flow[i, j] = flow[j, i] = rng.integers(0, 100)

print(flow)

[[ 0 72 10 92 87 31 48 79  4 17]
 [72  0 79 56 93 68 47 63 61 80]
 [10 79  0 84  8 43 32 97 17 44]
 [92 56 84  0  2 65 79 25 86 99]
 [87 93  8  2  0 77  5  4 50 34]
 [31 68 43 65 77  0  0 82 50 62]
 [48 47 32 79  5  0  0 14 16 81]
 [79 63 97 25  4 82 14  0 91 88]
 [ 4 61 17 86 50 50 16 91  0 74]
 [17 80 44 99 34 62 81 88 74  0]]

Amplify SDK による定式化

Amplify SDK による定式化を行います。定式化において、どの 2 つのバイナリ変数からなる 2 次項も目的関数に現れるので、Matrix クラスを使うと効率的な定式化を行うことができます。

変数の作成

Matrix クラスを使用した定式化を行うためには、VariableGenerator の matrix() メソッドを使用して変数を発行します。

from amplify import VariableGenerator

gen = VariableGenerator()
matrix = gen.matrix("Binary", N, N)  # coefficient matrix
q = matrix.variable_array  # variables

q

\[\begin{split}\displaystyle \begin{aligned}&\left[\begin{matrix}q_{0,0}& q_{0,1}& q_{0,2}& q_{0,3}& q_{0,4}& q_{0,5}& q_{0,6}& q_{0,7}& q_{0,8}& q_{0,9}\\q_{1,0}& q_{1,1}& q_{1,2}& q_{1,3}& q_{1,4}& q_{1,5}& q_{1,6}& q_{1,7}& q_{1,8}& q_{1,9}\\q_{2,0}& q_{2,1}& q_{2,2}& q_{2,3}& q_{2,4}& q_{2,5}& q_{2,6}& q_{2,7}& q_{2,8}& q_{2,9}\\q_{3,0}& q_{3,1}& q_{3,2}& q_{3,3}& q_{3,4}& q_{3,5}& q_{3,6}& q_{3,7}& q_{3,8}& q_{3,9}\\q_{4,0}& q_{4,1}& q_{4,2}& q_{4,3}& q_{4,4}& q_{4,5}& q_{4,6}& q_{4,7}& q_{4,8}& q_{4,9}\\q_{5,0}& q_{5,1}& q_{5,2}& q_{5,3}& q_{5,4}& q_{5,5}& q_{5,6}& q_{5,7}& q_{5,8}& q_{5,9}\\q_{6,0}& q_{6,1}& q_{6,2}& q_{6,3}& q_{6,4}& q_{6,5}& q_{6,6}& q_{6,7}& q_{6,8}& q_{6,9}\\q_{7,0}& q_{7,1}& q_{7,2}& q_{7,3}& q_{7,4}& q_{7,5}& q_{7,6}& q_{7,7}& q_{7,8}& q_{7,9}\\q_{8,0}& q_{8,1}& q_{8,2}& q_{8,3}& q_{8,4}& q_{8,5}& q_{8,6}& q_{8,7}& q_{8,8}& q_{8,9}\\q_{9,0}& q_{9,1}& q_{9,2}& q_{9,3}& q_{9,4}& q_{9,5}& q_{9,6}& q_{9,7}& q_{9,8}& q_{9,9}\end{matrix}\right]\end{aligned}\end{split}\]

目的関数の作成

上で作成した matrix は Matrix クラスのインスタンスであり、

• quadratic

• linear

• constant

の 3 種類のプロパティを持ちます。

quadratic は 2 次の項の係数を表す numpy.ndarray で、その shape は今回は (N, N, N, N) となっています。quadratic[i, k, j, l] は q[i, k] * q[j, l] の係数に対応します。つまり quadratic には quadratic[i, k, j, l] = distance[i, j] * flow[k, l] となるように 4 次元 NumPy 配列を設定する必要があります。

linear と constant はそれぞれ線形項の係数と定数項を表しますが、今回使用する目的関数には 2 次の項しか含まれないため、設定しません。

np.einsum("ij,kl->ikjl", distance, flow, out=matrix.quadratic)

制約条件の作成

変数の作成 で作成した変数配列 q の各行各列に one-hot 制約をかけます。

from amplify import one_hot

constraints = one_hot(q, axis=1) + one_hot(q, axis=0)

組合せ最適化モデルの作成

目的関数と制約条件を組み合わせて、モデルを作成します。

penalty_weight = np.max(distance) * np.max(flow) * (N - 1)
model = matrix + penalty_weight * constraints

制約条件に penalty_weight をかけているのは、制約条件に重みをつけるためです。今回使用するソルバーである Amplify AE においては、制約条件に適切な重みを指定しないと、ソルバーが制約条件をみたそうとするよりも目的関数を小さくする方向に動いてしまい、良い解を発見することができなくなってしまいます。詳しくは 制約条件とペナルティ関数 を参照してください。

ソルバークライアントの作成

Amplify AE を用いて組合せ最適化を実行するために、ソルバークライアントを作成します。Amplify AE に対応するソルバークライアントクラスは AmplifyAEClient クラスです。

from amplify import AmplifyAEClient

client = AmplifyAEClient()

Amplify AE の実行に必要な API トークンを設定します。

Tip

ユーザ登録を行うと、評価・検証目的に使える API トークンを無料で入手できます。

client.token = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"

ソルバーのタイムアウト値を設定します。

import datetime

client.parameters.time_limit_ms = datetime.timedelta(seconds=1)

求解の実行

作成した組合せ最適化モデルとソルバークライアントを使用してソルバーの実行を行い、二次計画問題の解を求めます。

from amplify import solve

result = solve(model, client)

目的関数の値は以下のように表示できます。

result.best.objective

170644.7865651759

最適解における変数の値は、NumPy の多次元配列の形式で以下のようにして取得できます。

q_values = q.evaluate(result.best.values)

print(q_values)

[[0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]
 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]]

結果の確認

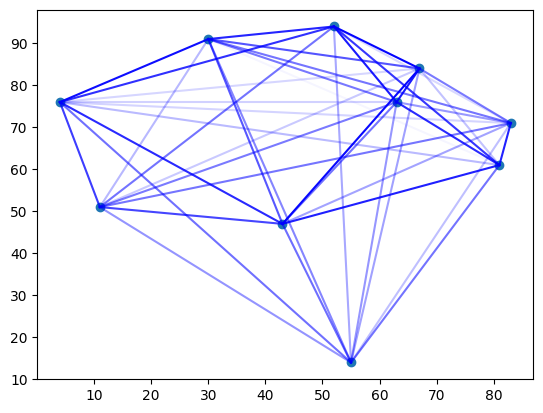
matplotlib を用いて結果を可視化します。

import itertools

import matplotlib.pyplot as plt

plt.scatter(x, y)
factory_indices = (q_values @ np.arange(N)).astype(int)

for i, j in itertools.combinations(range(N), 2):
    plt.plot(
        [x[i], x[j]],
        [y[i], y[j]],
        c="b",
        alpha=flow[factory_indices[i], factory_indices[j]] / 100,
    )