Tutorial

はじめに

Amplify SDK はイジングマシンを手軽に扱うためのミドルウェアライブラリです。イジングマシンとは、イジング模型あるいは QUBO模型と呼ばれる、二値変数の多項式の最小化問題に対する専用のハードウェアです。下記はQUBOによる表現例になります。

\[f = \sum_{i < j}{Q_{i,j} q_i q_j} + \sum_{i}{Q_{i,i} q_i} \quad \left(q_i \in \left\{ 0, 1\right\} \right)\]

通常、イジングマシンを実行するためには「対象となる最適化問題」を「実行するイジングマシンに入力可能な形式」に変換する必要があります。なぜなら多くのイジングマシンは、バイナリ変数 \(\left\{0, 1\right\}\) またはイジング変数 \(\left\{-1, 1\right\}\) の二次多項式 (論理模型) のみを入力形式とし、イジングマシンによっては任意の二次多項式を扱えるわけではなく、ハードウェア仕様に起源する変数間のグラフ構造に従った形式 (物理模型) で表現する必要があるためです。

ユーザが対象とする最適化問題 (入力模型) をイジングマシンで実行する場合、入力模型から論理模型に変換し、さらに論理模型を各イジングマシンに固有の物理模型に変換するという手順を踏みます。一方、イジングマシンの出力値を解釈するために、この手順の逆変換を各々のステップに施します。この変換・逆変換処理では、変換に伴う制約条件等の「前処理」や出力値の逆変換に伴う制約条件の充足検査等の「後処理」もまた重要になります。

Amplify SDK は最適化問題をイジングマシンで実行するための統合インタフェースを提供し、入力模型や各イジングマシンの仕様に依存した変換・逆変換や前処理・後処理を隠蔽します。また、入力模型の作成や結果の解釈を行うための支援機能を提供します。Amplify SDK のアーキテクチャについてはリファレンス [1] を参照してください。次の図は Amplify SDK によるイジングマシンへの入力から実行及び結果の解釈までのフローを表します。

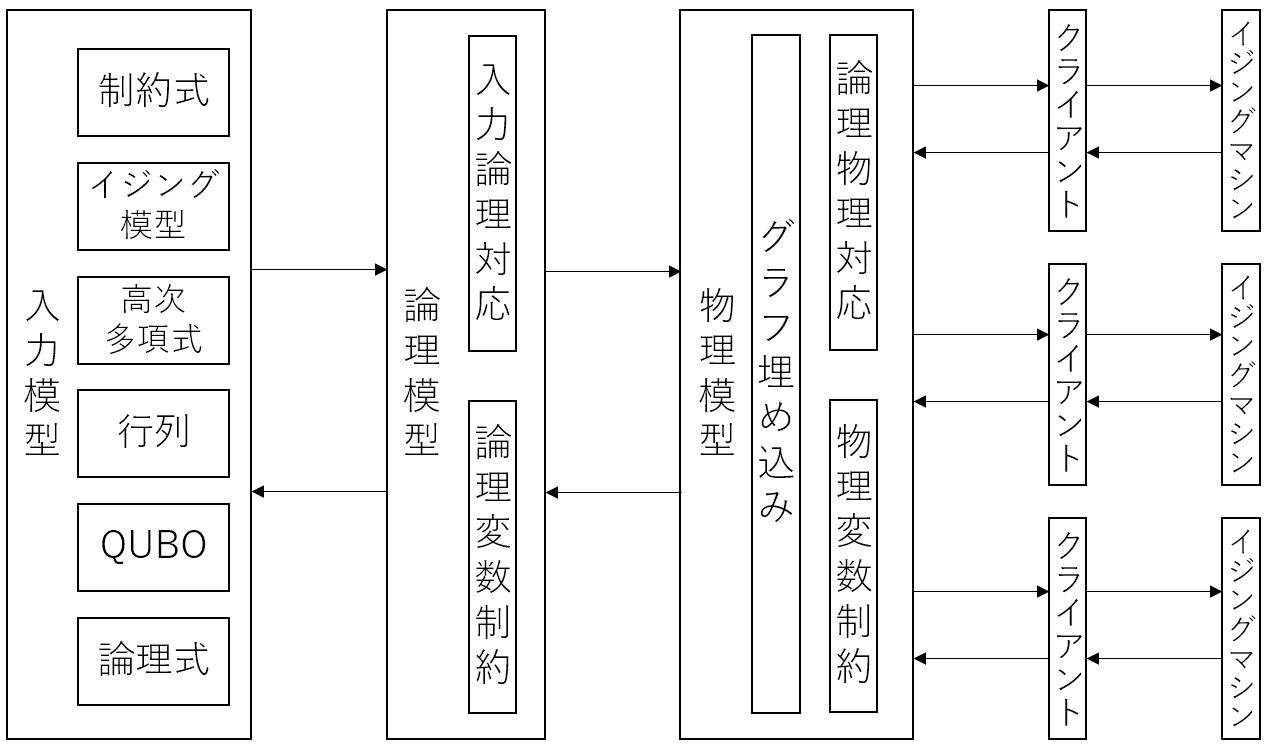
各フローと Amplify SDK が提供するクラスの対応関係は次の通りです。

入力レイヤ

ユーザがイジングマシンへの「入力模型」として直接操作を行います。下記の数式オブジェクトを取り扱うことが出来ます。

多項式:: BinaryPoly, IsingPoly, BinaryIntPoly, IsingIntPoly
多項式配列:: BinaryPolyArray, IsingPolyArray, BinaryIntPolyArray, IsingIntPolyArray
行列:: BinaryMatrix, IsingMatrix BinaryIntMatrix, IsingIntMatrix
制約式:: BinaryConstraint, IsingConstraint, BinaryIntConstraint, IsingIntConstraint

論理レイヤ

構築した入力模型をイジングマシンが取り扱うことが可能な「論理模型」として抽象化します。

二次多項式模型:: BinaryQuadraticModel, IsingQuadraticModel, BinaryIntQuadraticModel, IsingIntQuadraticModel

物理マシンレイヤ

最適化ソルバーが使用するハードウェア仕様に基づいて論理模型を「物理模型」に変換します。ユーザが直接変換コードを記述する必要はなく、各マシンの実行パラメータの操作のみを行います。

最適化ソルバー:

Solver

マシンクライアント:

Fixstars:: FixstarsClient
D-Wave:: DWaveSamplerClient, LeapHybridSamplerClient
Fujitsu:: FujitsuDASolverClient, FujitsuDASolverExpertClient, FujitsuDAPTSolverClient, FujitsuDAMixedModeSolverClient, FujitsuDA2SolverClient, FujitsuDA2SolverExpertClient, FujitsuDA2PTSolverClient, FujitsuDA2MixedModeSolverClient, FujitsuDA3SolverClient
Toshiba:: ToshibaClient
Hitachi:: HitachiClient
Hiroshima Univ. / NTT DATA:: ABSClient
Gurobi:: GurobiClient

Amplify SDK によるプログラミングフロー

Amplify SDK を使用したイジングマシン使用の流れは次の通りです。

対象となる最適化問題を定式化し入力模型を作成する (入力レイヤ)
入力模型を二次多項式模型に変換する (論理レイヤ)
使用するマシンを宣言しパラメータ設定を行う (物理マシンレイヤ)
最適化ソルバーに論理模型を与えて入力模型に逆変換された実行結果を得る

ここからは、上記に従い各レイヤでの Amplify の実際の使用手順について説明します。

まずは上述の「入力模型」の取り扱いについて説明します。最も単純な例題として、下記のバイナリ変数 \(\left\{0, 1\right\}\) についての関数 (バイナリ変数の多項式) の最小化問題を取り上げます。

\[f\left( q_0, q_1 \right) = 1 - q_0 q_1\]

\(q_0, q_1 \in \left\{ 0, 1 \right\}\) なので自明に \(f \left( q_0 = 1, q_1 = 1 \right) = 0\) が最適値となります。ここから実際にこの問題をイジングマシンに入力し、最適解が出力されるかを確認していきます。

バイナリ変数の多項式をプログラムコード上で表現するために BinaryPoly クラスが提供されています。

BinaryPoly の構築にはいくつか方法がありますが、必要な変数の集合を配列 \(\mathbf{q} = \left\{q_0, q_1, ... \right\}\) として用意してから多項式を構築する方法が簡単です。

まず、変数の配列は SymbolGenerator() クラスを用いて次のようにして生成出来ます。

from amplify import BinaryPoly, SymbolGenerator

gen = SymbolGenerator(BinaryPoly)  # 変数変数ジェネレータを定義
q = gen.array(2)  # 長さ2の Binary 配列を生成

>>> q
[q_0, q_1]

バイナリ変数 (BinaryPoly) の変数インデックス \(0\) から長さ \(2\) の一次元配列を作成しました。これを用いて次のように多項式を組み立てます。

f = 1 - q[0] * q[1]

>>> f
- q_0 q_1 + 1

変数配列を生成して構築する方法を用いると、プログラムコード上で配列名とそのインデックスを使用してシステマティックに多項式を構築することが可能です。より高度な問題では、複数の変数をまとめて扱うことになるため、配列を宣言してから定式化すると個々の変数について管理する必要がなくなり、見通しが良くなります。複数の配列やスカラー変数も管理することが出来ます。詳細は変数配列を用いた構築を参照してください。

注釈

二次多項式に限らず三次以上の高次多項式の構築も可能です

論理模型への変換

次に入力模型から論理模型を構築します。今回は BinaryPoly を入力として持つので、論理模型として BinaryQuadraticModel に変換します。論理模型への変換は、単純な模型の場合は後述の最適化ソルバークラス Solver にて暗黙的に行うことも可能ですが、ここでは下記の様に明示的に model 変数で構築します。

from amplify import BinaryQuadraticModel

model = BinaryQuadraticModel(f)

論理模型の構築には、多項式以外にも行列や制約式を扱えます。また、多項式と制約式、行列と制約式、といった組合せで与えることも可能です。論理模型の内部表現や内部状態についてはいくつかのメソッドで取得が可能ですが、このチュートリアルでは割愛します。

注釈

多項式や行列と制約式の組合せについては論理模型オブジェクトの構築を参照してください。

実行するイジングマシンの設定

次に使用するイジングマシンのパラメータを設定します。ここでは Amplify Annealing Engine (FixstarsClient) を例として設定します。

from amplify.client import FixstarsClient

client = FixstarsClient()
client.token = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
client.parameters.timeout = 1000    # タイムアウト1秒

注釈

xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx には Amplify Annealing Engine のアクセストークンを入力して下さい。無料ユーザ登録を行うことでアクセストークンが発行されます。

注釈

他のクライアントを使用する場合のパラメータは Client を参照してください。

組合せ最適化の実行

以上で準備は完了です。次のようにして、最適化ソルバー Solver にクライアントを設定し、solve() メソッドを呼ぶことでイジングマシンが実行されます。マシンに依っては複数の解が出力されますが、通常は先頭から取り出すと良い解が取得できます。今回はシンプルなバイナリ変数の多項式を入力模型としましたが、制約式を与えた場合には制約を満たす解だけがフィルタされて出力されます。

from amplify import Solver

solver = Solver(client)
result = solver.solve(model)
for solution in result:
    print(f"energy = {solution.energy}\nvalues = {solution.values}")

energy = 0.0
values = {1: 1, 0: 1}

表示された値のうち energy は入力模型の \(f\) の値を、values は入力インデックスと変数の値を表す辞書を表します。つまり今回表示されている解は \(f\left( q_0 = 1, q_1 = 1 \right) = 0\) を意味します。これは最初に想定した最適解と一致します。

入力変数と出力変数を関係づけるために decode() メソッドを使用すると便利です。この関数はマシンの出力値をデコードし入力模型の構築時に使用した変数配列の形式に変換します。

for solution in result:
    print(f"q = {q.decode(solution.values)}")

q = [1. 1.]

変数配列 q に対して入力インデックスと変数の値を表す辞書 values が適用されました。これにより入力模型の構築に使用した配列と同様の形式で解の解釈を行うことが効率的に可能となります。

最後に上記のステップをまとめます。これが Amplify SDK を用いたイジングマシン実行のコードテンプレートになります。

from amplify import (
    BinaryPoly,
    BinaryQuadraticModel,
    Solver,
    SymbolGenerator,
)
from amplify.client import FixstarsClient

# 変数配列の生成
gen = SymbolGenerator(BinaryPoly)
q = gen.array(2)

# バイナリ多項式の構築
f = 1 - q[0] * q[1]
model = BinaryQuadraticModel(f)

# イジングマシンクライアントの設定
client = FixstarsClient()
client.token = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx"
client.parameters.timeout = 1000  # タイムアウト1秒

# ソルバーの実行
solver = Solver(client)
result = solver.solve(model)

# 結果の解析
for solution in result:
    print(f"q = {q.decode(solution.values)}")

次のステップ

以上が Amplify SDK を用いたプログラミングの基本的な流れです。

具体的な問題に対するサンプルコードについてはデモ・チュートリアルページを参照して下さい。

引き続きチュートリアルを読み進めたい場合や、より高度な使用方法については次セクション以降を読み進めてください。最適化問題の様々な形式による構築方法や、このセクションで取り上げた各クラスの持つ機能の詳細を説明します。クラスや関数の形式的なリファレンスは Reference にまとめられています。